Irrelevant Topics II
in Physics
Topics:
Extraordinarily Large Numbers
Mathematical Notation
Venn-Diagrams
Logic, Set Theory
Extraordinarily Large Numbers
they're just big boned
First a contest!
- Write the largest number you can think of on the note card.
- Use standard mathematical functions or define your own.
- The number must be completely defined on the card.
- The number must be verifiably finite and computable.
Progression of expression
- First-grader:
- Third-grader:
- Sixth-grader:
Twelfth-grader
What's next?
Addition, multiplication and exponentiation are
simply higher orders of the same function:
Knuth's Up-Arrow notation
Each arrow starting from exponentiation
forms the higher operators
Numerical examples (the operator is right-associative):
More arrows!
We can grow larger numbers by simply
adding more arrows onto the expression
Time to think big

The idea is not to generate the largest number,
per se, but rather the largest growing function...
Many different styles: Conway's chained arrow,
hyper-geometric, and of course, Knuths Up-Arrow
Why are big numbers so awesome?
We have primitive brains. For small numbers we can only think
spatially, 4 cows, 3 hens etc... Abstract numerical systems
allow us understand larger quantities.
If you build it... large numbers systems
were invented because of their necessity.
Grahams number
Grahams number is so big that even Knuths up arrow notation
is insufficient to contain it. It is the best known
upper-bound to the problem:
- Consider an n-dimensional hypercube, and connect each pair of vertices to obtain a complete graph on vertices. Then color each of the edges of this graph using only the colors red and black. What is the smallest value of n for which every possible such coloring must necessarily contain a single-colored complete sub-graph with 4 vertices which lie in a plane?
Grahams number,
This is an upper bound to the problem. It has been proven that the lower bound solution is at least 11. The authors (modestly) state that there is some room for improvement.
Venn-diagrams
Inclusion-exclusion principle (extreme)
You, at the conclusion of this talk
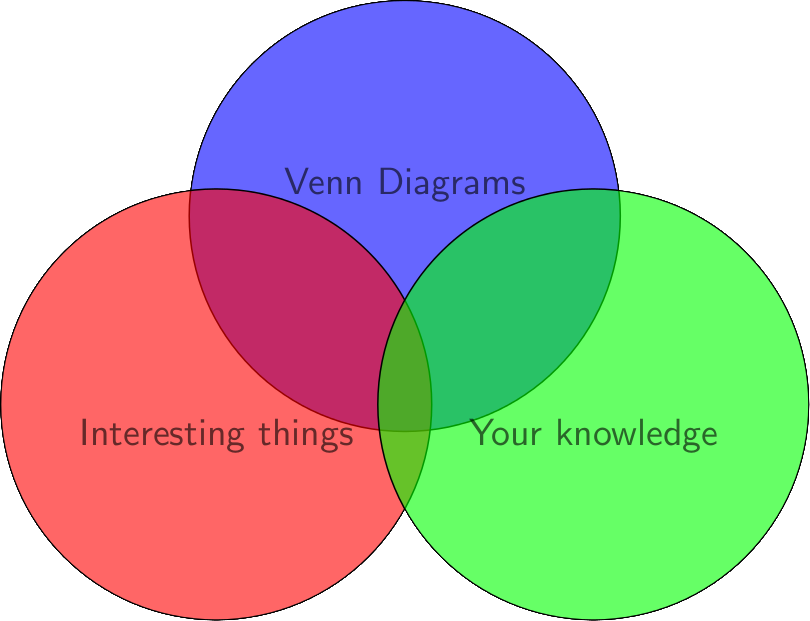
(originally invented by Euler)
Formal definition of a Venn Diagram
Let be a collection of simple closed curves drawn in the plane. The collection is said to be an independent family if the region formed by the intersection of is nonempty, where each is either the interior or exterior of .
If, in addition, each such region is connected and there are only finitely many points of intersection between curves, then is a Venn diagram, or an -Venn diagram if we wish to emphasize the number of curves in the diagram.
In other words every subset built from a collection of n objects has to be represented only once.
Not Venn
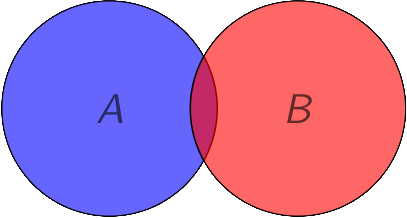
Not Venn as is not represented.
Still known as an Euler diagram.
Converting diagrams to graphs
Constructing graphs allows different Venn diagrams of the same order to be compared. Diagrams are isomorphic if their graphs are isomorphic.
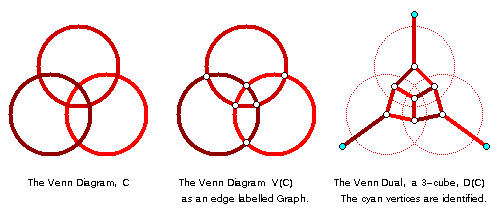
Special Venn Diagrams: Minimum
Number of vertices in the graph is no more than:
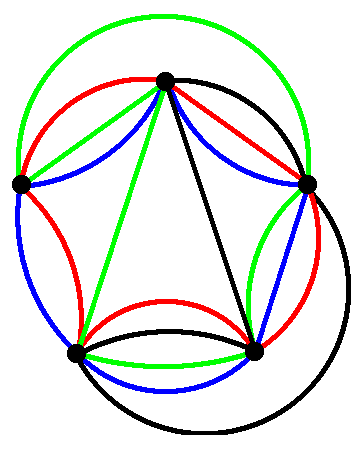
Special Venn Diagrams: Symmetric
Must display n-fold symmetry.
Can be shown that these only exist when n is prime.
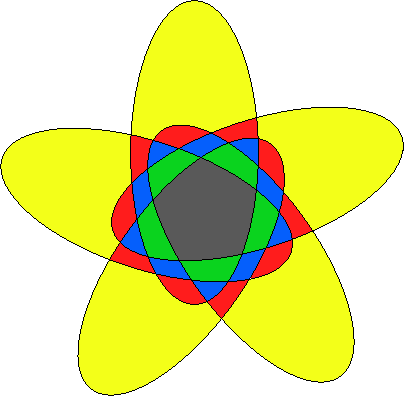
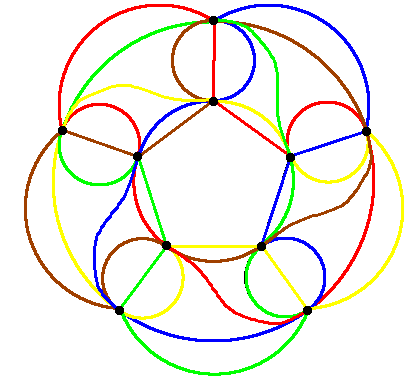
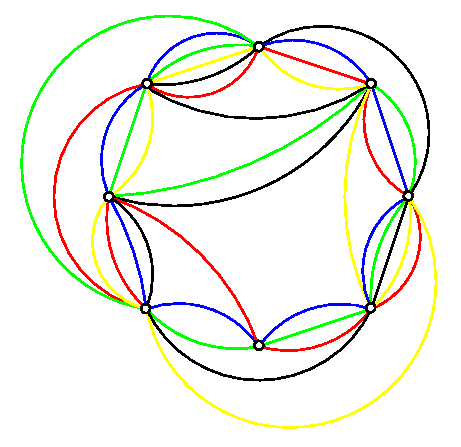
Large Venns: Seven region Venn
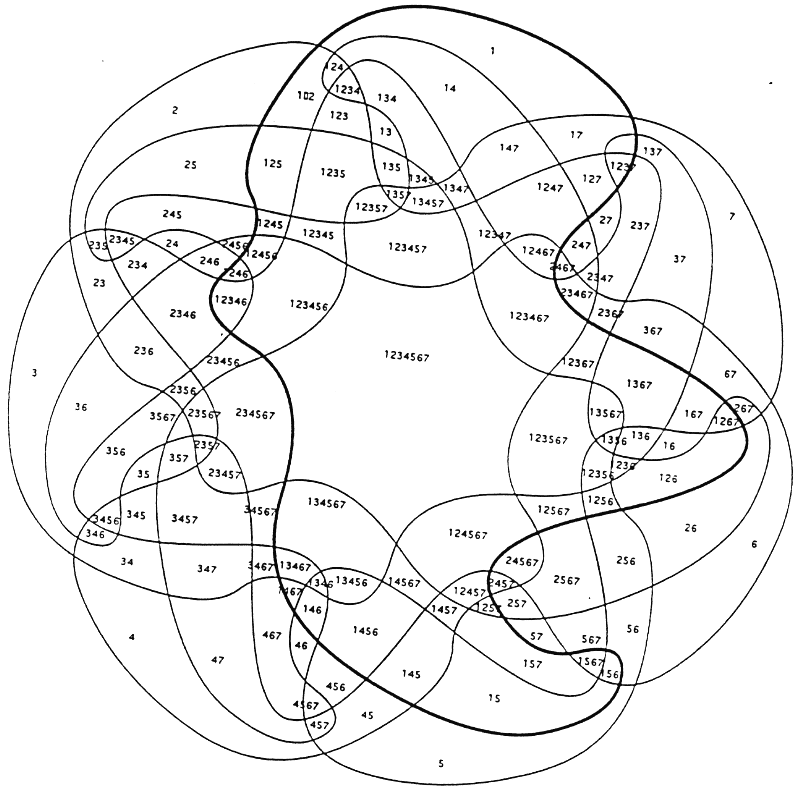
Large Venns: Seven region Venn
Ugly, but formulaic way to create higher orders