Irrelevant Topics III
in Physics
Topics:
Cardinality of Infinity
Set theory
Negative Probabilities
Physics
Hobomorphism
Graph Theory
Cardinality
of Infinity
plus one
What is a distance?
For physicists, a distance is the norm
More than one type of norm,
Set theorists think of counting,
the cardinality of a set.
Finite sets
Size of the set = number of objects in it
Infinite set?
Comparisons can still be made.
Sets are equal, iff they can be put in a one-to-one
correspondence with each other.
Even numbers have the same cardinality
as the natural numbers
we show this with a bijection
This holds for all infinite partitions of the
natural numbers (odds, divisible by 13, primes, etc...)
Countable Sets
Rational numbers also have the
same cardinality as the natural numbers!

Cantor's diagonal line, omit repeats to get the mapping
Do all infinite sets have the same cardinality?
NO!
There are more reals then rationals!
Any subset of the real numbers i.e. [0,1] can be put
in correspondence with any other subset, or even the entire line.
The above is known as the continuum hypothesis, which can
neither be proved or disproved when assuming the axiom of choice.
Proof by contradiction, assume a mapping exists, for example take:
1 -> .47382474
2 -> .12030249
3 -> .24985283
4 -> .85472378Each real on the right is infinite, and the length of this list is also infinite. Take a diagonal of the list (.4297...) and add one to each of the numbers mod 10 (.5308...)
This new number is NOT on the list above, as it differs from the first digit
for the first number, second digit for the second number, etc...
The cardinality of the square is equal to a line segment.
Higher order cardinalities always exist by taking multisets,
The set of all sets:
multiset({1,2,3}) = {{}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}
What is the multiset of , , ...,
what about the multiset of multisets...?
What is the cardinality of reality?
Sets of higher order then the real numbers
have never found use in physics.
However, the language of quantum mechanics uses
discrete (quanta of energy, spin, ...) and
continuous variables (position, momenta, ...).
Negative Probabilities
The worst gambling odds
Relax the assumption that each probability must be positive.
Relax the assumption that each probability must be less than one.
Still enforce that the sum of all events must be unity.
What's left?
Feynman's Roulette
Consider a concrete example of a strange roulette wheel. The table is known to have three observable states, and two internal (non-observable states) with stochastic probability of coming up:
A(.7) B(.3)
----------------
1 | 0.3 -0.4
2 | 0.6 1.2
3 | 0.1 0.2Possible that the direct states of the system are not observable:
Why not rearrange the calculation or theory
so probabilities are positive in all intermediate states?
The accountant who subtracts all payments before adding
in the profits (intermediate sum can be negative).
Nothing wrong mathematically when working
with negative probabilities.
Hobomorphism
A Solution to Graph Isomorphism
What train-hopping hobos can teach us
Hobos on a Train
A Hobo is a term that refers to a subculture of wandering homeless people, particularly those who make a habit of hopping freight trains - wikipedia

Hobosumptions
Assume that occasionally, when a hobo wakes up,
he is unsure of his current location.
As a survival instinct, he has memorized all
the train schedules for each country.
Wine has degraded his memory,
he only remembers the connections.
Hobomaps
It is crucial when picking up a train schedule,
no matter what country, to determine the lay of the land.
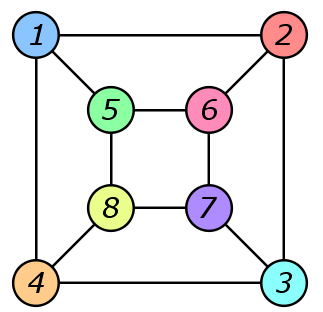
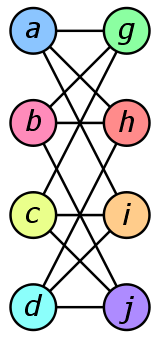
Are the graphs the same (isomorphic) or different?
Hobomath
A mathematician would call the hobo-map an undirected,
unlabeled simple graph, where the process for determining
two graphs are the same is known as graph isomorphism.
Computationally, graph isomorphism is curious,
it belongs to but it is not known to have
a polynomial solution (), nor is it -complete.
An invariant is a graph property that can (possibly) show
two graphs different, e.g. number of nodes, degree sequence,
number of edges, etc... Graphs with different invariants are
not isomorphic; the converse is NOT true in general.
Adjacency Matrix
For an undirected graph it is a symmetric matrix withif nodes are joined by an edge and zero otherwise.
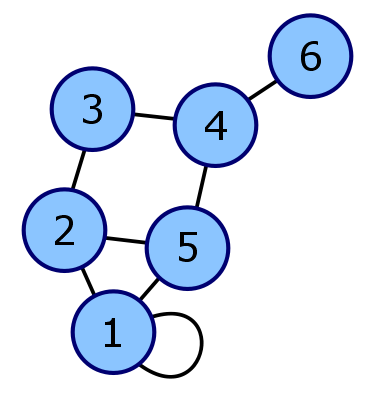
Generating Functions
This matrix has nice properties. Raised to a power the element
tells you the number of trips starting at and ending at
of length . A GF can be found that gives all the terms of :
This step is assumed to be a polynomial time operation. Finding of matrix can be doing using LU decomposition by dividing and multiplying rows. When the matrix elements themselves are polynomials, the number of operations is surely increased, but (seems to be) bounded by polynomial time.
Symmetric Nodes
Once each generating function is found, it encodes all the powers of into it by taking higher terms of . If two nodes share the property:
We call them symmetric. The unordered set is a graph invariant:
Sets of nodes share the same generating function
Hobomorphism
Does this set uniquely define a graph?
Can one produce a graph simply by knowing how many walks
of length lead back home for all and for all nodes?
If so, the graph isomorphism problem has a polynomial time solution.
Graph isomorphism,
dangerously relevant?
- Computationally an unsolved problem.
- Chemical structure evaluations.
- Symmetric groups for coupled Josephson-Junction systems.
- Discrete mathematics: knights tours, Rubik's Cube, etc...
- Solid state lattice structures