Irrelevant Topics IV

in Physics



Travis Hoppe
(deck source)

Topics:


Esoteric Programming Languages

Computer Science


ChutesAndLadders

Board Games, Physics

Esoteric programming languages

Not your grandpa's Turing machine

Esolang and You

Why learn an esoteric language?


  • To push the boundaries of code/computation.
  • Examine the fundamental idea of an algorithm.
  • Has been done before with information, cf. Shannon.
  • Test computability, are non-computable ideas unphysical?
  • Central Irrelevant Topics Paradigm: Divide by zero.

Grandpas Turing Machine



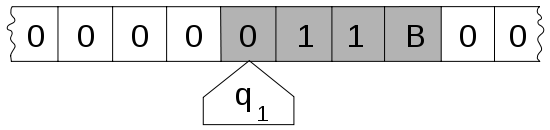
A infinite "tape" of finite symbols.


A "head" with an internal state that
can advance only one spot at a time.


A finite set of instructions:
given a state and symbol perform set action.

Church Turing:

Every Universal Turing Machine is equivalent to every other


Turing Complete

Once a language can be shown to be similar to the tape-machine it is identical from a computational standpoint to any other.

Turing Tar Pits


  • Embody the idea of Turing's original tape machine.
  • (very) Limited set of instructions.
  • (very) Limited set of symbols.
  • Create obfuscated, impossible to maintain codes.
  • Extremely simple compilers.
  • Serves as a model to construct higher-order languages.

Funges


  • Extension of one-dimensional Turing tape machine.
  • Live in metric spaces with coordinate systems.
  • Usually Cartesian, but not necessarily.
  • Considered a "funge" if topology is toroidal.
  • More exotic topologies are classified as fungeoids.

Brainf*ck


  • Extreme minimalism: Turing tarpit
  • Designed to challenge and amuse programmers
  • Not suitable for practical use
  • Smallest compiler only 200 bytes!

Brainf*ck Instruction Set


  • > increment the data pointer
  • < decrement the data pointer
  • + increment the byte at the data pointer
  • - decrement the byte at the data pointer
  • . output the value of the byte at the data pointer
  • [ if the byte at the data pointer is zero, then instead of moving the instruction pointer forward to the next command, jump it forward to the command after the matching ] command.
  • ] if the byte at the data pointer is nonzero, then instead of moving the instruction pointer forward to the next command, jump it back to the command after the matching [ command.
  • , accept one byte of input, storing its value in the byte at the data pointer.

Brainf*ck Sample Code


Hello World

++++++++++[>+++++++>++++++++++>+++>+<<<<
-]>++.>+.+++++++..+++.>++.<<+++++++++++++++
.>.+++.------.--------.>+.>.

The first line initializes a[0] = 10 by simply incrementing ten times from 0. The loop from line 2 effectively sets the initial values for the array: a[1] = 70 (close to 72, the ASCII code for the character 'H'), a[2] = 100 (close to 101 or 'e'), a[3] = 30 (close to 32, the code for space) and a[4] = 10 (newline). The loop works by multiplying the value of a[0], 10, by 7, 10, 3, and 1, saving the results in other cells. After the loop is finished, a[0] is zero. >++. then moves the pointer to a[1] which holds 70, adds two to it (producing 72 which is the ASCII character code of a capital H), and outputs it.

Befunge


  • Stack-based, Turing-tape style language.
  • Programs are arranged on a two-dimensional grid.
  • Tape has the topology of a toroid.
  • Arrow instructions direct the control flow.
  • Loops are constructed by sending the control flow in a cycle.
  • Befunge is a proper funge, and higher dimensional funges exist such as Trefunge.

Befunge Sample Code


Hello World

vv  <      <
    2
    ^  v<
 v13v4
    ^   ^
>  >?>  ?>5^
    v   v
 v97v6
    v  v<
    8
 .  >  >   ^
^<

Whitespace


  • Ignores all characters but whitespace.
  • Each whitespace combination forms a bit-pattern.
  • Whitespace can be a polyglot.
  • Stenographic capabilities.
  • Challenges the idea of symbol and tape instructions.
  • Proof of Turning completeness is now CS homework.

Whitespace Sample Code


Hello World

 Say Hello

Non deterministic languages


Given the state of the program: the next action is taken
according to a probability distribution


Getting even trivial programs to have a reliable output is often a monumental task. Useful for exploring large search spaces, quantum computing, machine learning, ...


  • Unreliable (a feature not a bug!)
  • What is the notion of computability for a ND machine?
  • Expectation values of computability, Turing is a special case
  • Is Godel's incompleteness theorem even valid?

Chutes and Ladders

overthinking a classic

How many ideas of physics can be
expressed under the C&L topology?

Energy Landscapes


Chutes and Ladders Potential Function?


C&L does not possess a typical energy landscape; rather it is a stochastically driven process with discrete jumps.

Markov Chains

Used to represent transitions along discrete states, assumes
time-invariance. represents the probability from
state , and .

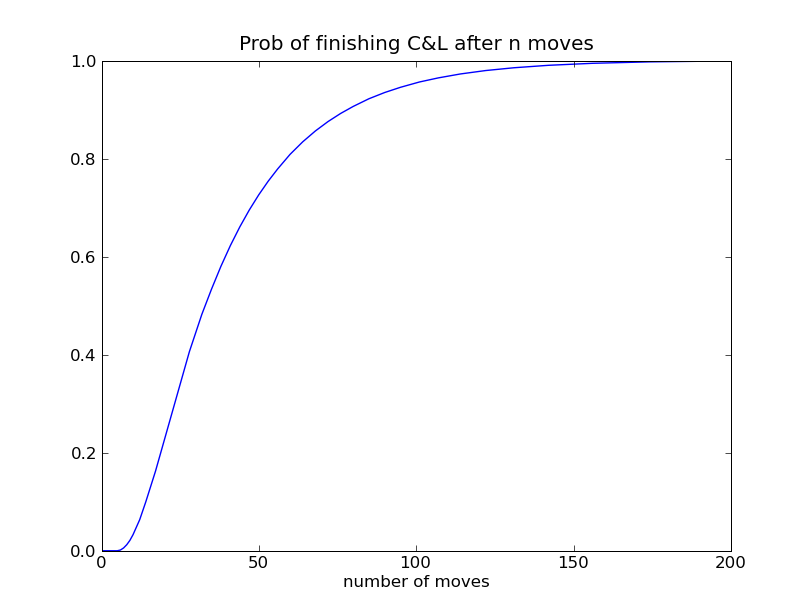
Single player Game Length Attention Span

Ergodic chain distributions

let the board become a loop, and look for steady state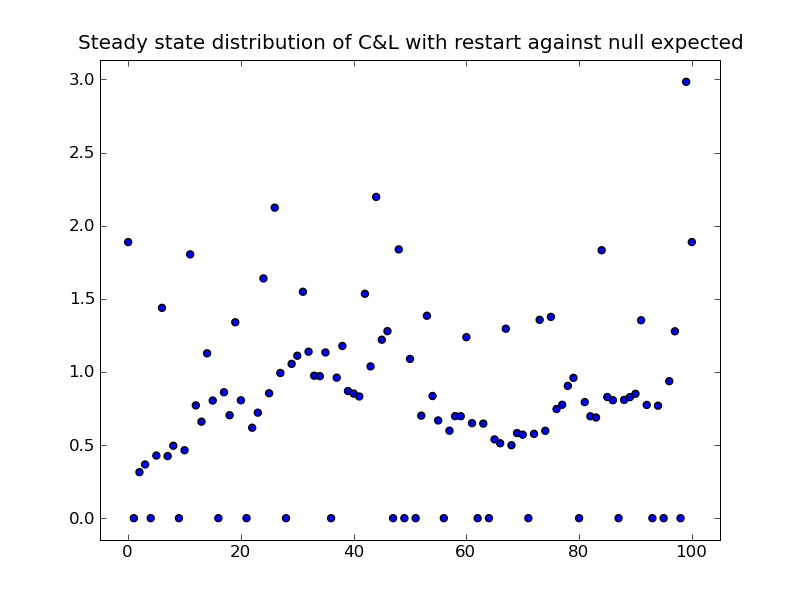

Approaching steady state



, , , , ,

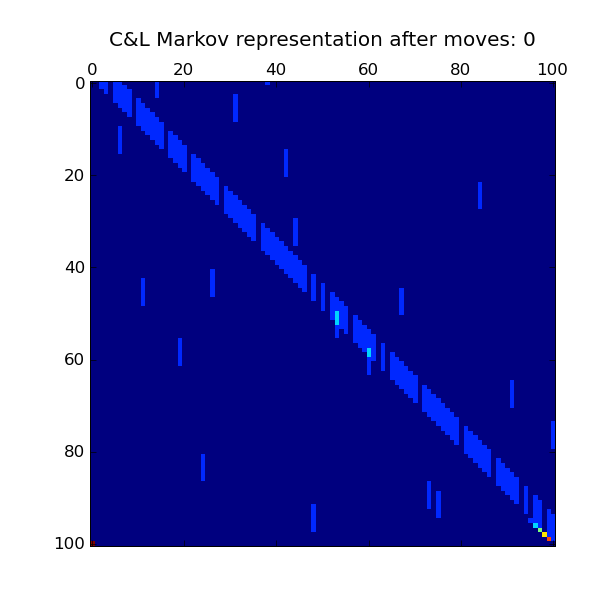
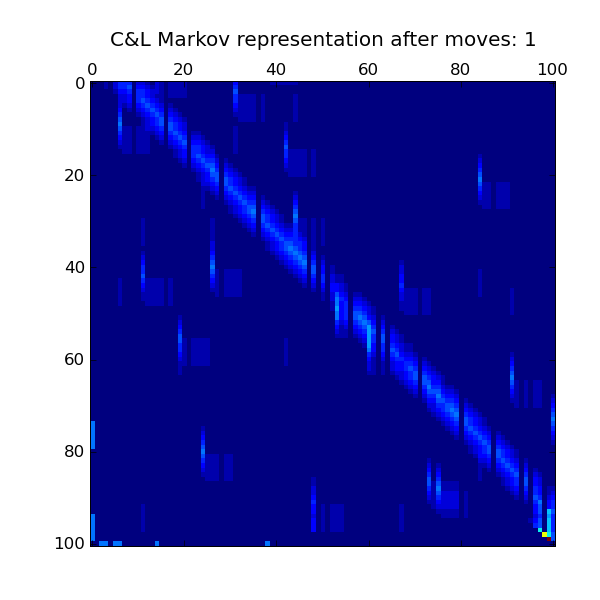
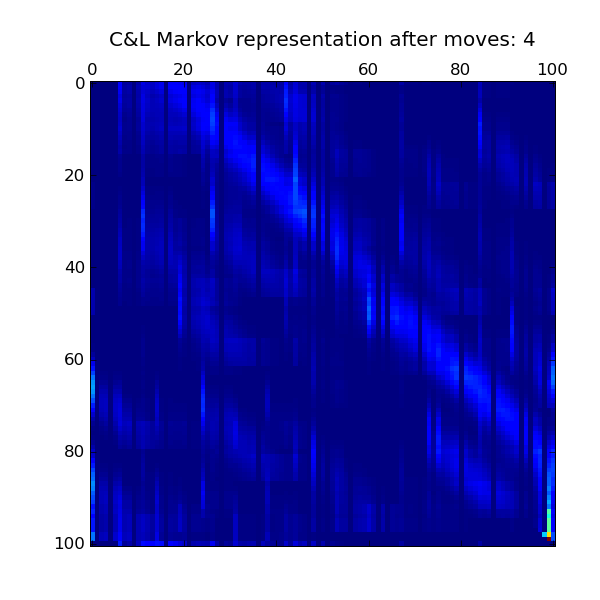
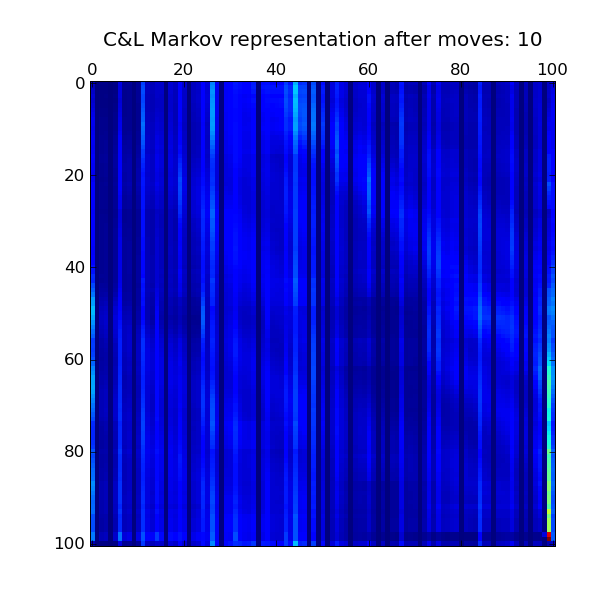
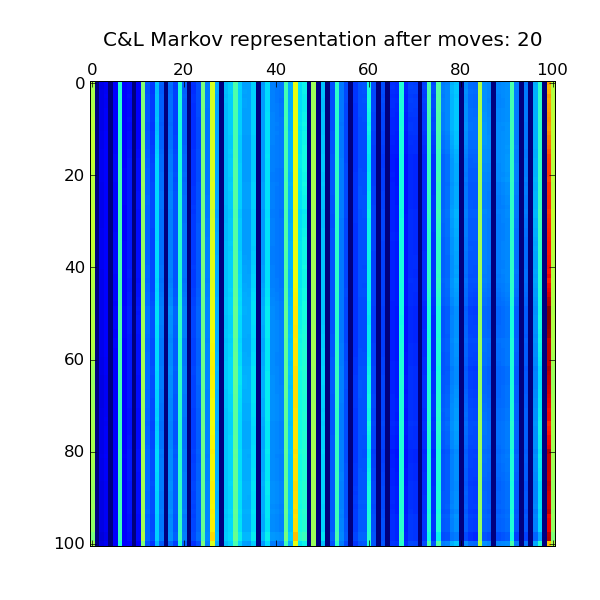
Differential Operators over C&L


Exponential Maps, and flows give rise to a differential-mapping. A set of coupled first-order differential equations has a natural connection to Markov chains:



The Markov matrix is the generator of the rate matrix at a given time:


Continuous-Time C&L


Assume that the die rolls now represent rates (like a chemical equation), i.e. the first roll would be:



This system of equations can be exponential to give a continuous-time Markov game.

['height:300px']


,


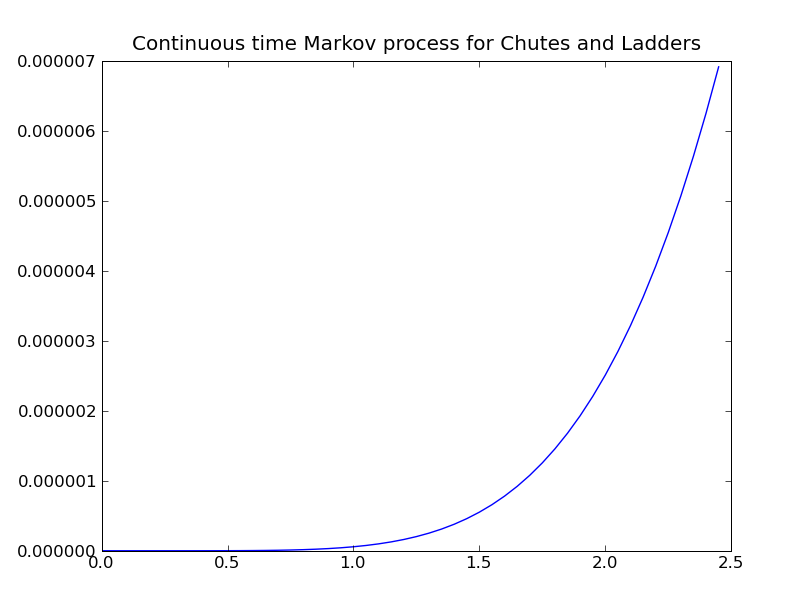
Note the abissica on the second picture,
we are modeling fractions of a die roll!