Irrelevant Topics VI
in Physics
Topics:
Cayley-Dickson Process
Abstract Algebra
Pseudospectra
Linear Algebra
Markov Cutoff Phenomenon
Stochastic processes
Cayley Dickson Process
Real numbers of ill-repute
The illustrious family
The real numbers are the dependable breadwinner of the family, the complete ordered field we all rely on. The complex numbers are a slightly flashier but still respectable younger brother: not ordered, but algebraically complete. The quaternions, being noncommutative, are the eccentric cousin who is shunned at important family gatherings. But the octonions are the crazy old uncle nobody lets out of the attic: they are nonassociative.
John Baez
Start Simple
Complex Numbers:
- "Officially" discovered by Cardano in solving the cubic
- Addition is element wise
- Think of them as ordered pairs of real numbers
- Multiplication:
- Complex Conjugate:
Descend into the rabbit-hole:
The complex numbers lack a property of the reals,
a real number unlike a complex one, is its own conjugate.
Quaternions:
Discovered by William Rowan Hamilton (yes that one).
Think of them as ordered pairs of real complex numbers.
Useful for calculations involving three-dimensional rotations
Pairs of unit quaternions represent a rotation in 4D space, SO(4)
In modern language, quaternions form a four-dimensional
normed division algebra over the real numbers
Conjugate:
The quaternions are non commutative:
Cayley-Dickson Process
Multiplication:
Conjugate:
These form the hypercomplex families under the CD process. With slight variations on the multiplication step you can get interesting forms like the split-complex, bi-complex, ..., etc.
Octonions
The octonions are non associative:
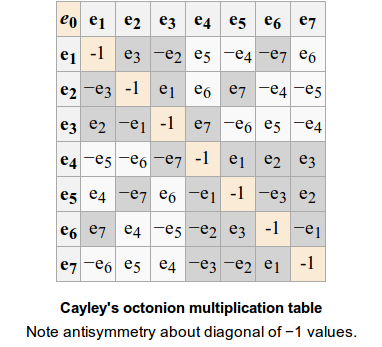
Octonions
They do however, retain a norm-property:
They still are "human", and have yet to descend into the madness that lies ahead. In fact only , and form finite-dimensional division algebras over the reals.
They are related to the exceptional Lie groups and have have applications in fields such as string theory, special relativity, and quantum logic.
Powwwwwwwweeeeeeeerrrr!
Represent Octonions in hypercomplex polar coordinates:
Called hyperexponential form or, informally:
The tower of power
Sedenions
Sedenions have Zero Divisors (ZD).
This is bad.
Really bad.
A ZD is a number such that , . When mathematicians are given a set, they ask what they can do with it. With a non-commutative, non-associative, algebra with zero-divisors the answer is ... not much. On the bright side, they are power associative: .
Zero Divisors
Sedenions multiplication table: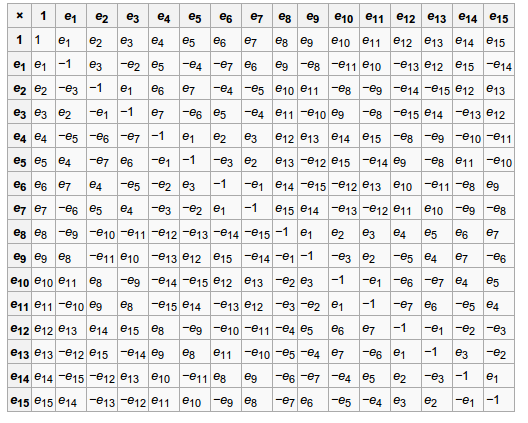
To infinity...
We can repeat the process and create:
trigintaduonions (32 D),
sexagintaquatronions (64 D),
centumduodetrigintanions (128 D),
ducentiquinquagintasexions (256 D)
Which were named to get away from the cumbersome Latin form:
pathions (32 D),
chingons (64 D),
routons (128 D),
voudons (256 D)
The prediction and properties of the zero-divisors
becomes an interesting study in it's own right!
Pseudospectra
Pseudo make me a sandwich?
Eigenvalues
Eigenvalues are defined by:
in other words, the undefined points of:
If is an eigenvalue then the above expression has a norm of infinity.
Pseudo-Eigenvalues
What if, is not infinite, but very large? Instead of a regular spectrum of eigenvalues, we get a pseudospectra:
An aside: There are a few ways to consider what means...
Never be normal!
If a matrix is normal, the pseudospectra is boring, they are simply circles in the complex plane. For non-normal matrices, it gets more interesting...
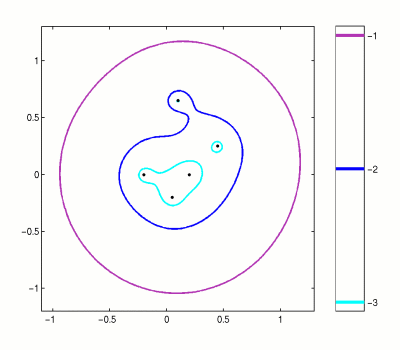
Unwanted growths
If all in a matrix then the iteration converges to zero as goes to infinity. However, the pseudospectra can predict if there is some (large) period of growth before the decay!
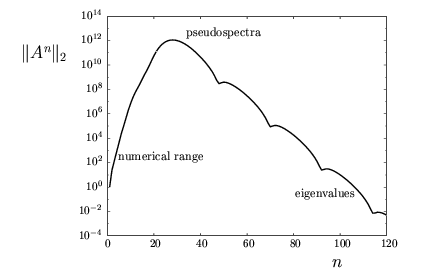
Markov Cutoff
Phenomenon
Surprisingly to getting drunk on a lattice
Markov Matrices
A Markov matrix has the following properties:
represents the probability of going from one state to another.
represents the probability of going from one state to another after time steps.
Examples
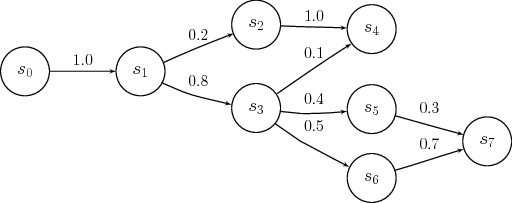
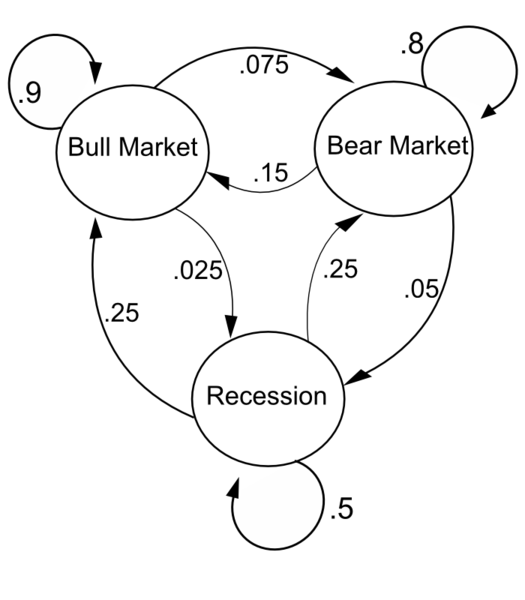
Stationary States
For most Markov matrices there exists a steady state:
for any starting vector , equivalent to writing a left-eigenvector .
What is more interesting is the decay matrix:
And consider the maximum element . This measures how "far away" we are from the steady-state distribution.
Example:
Hypercube
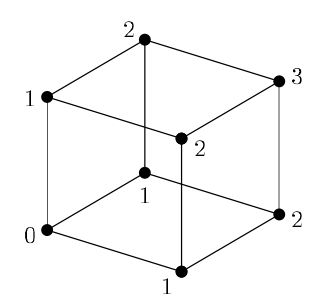
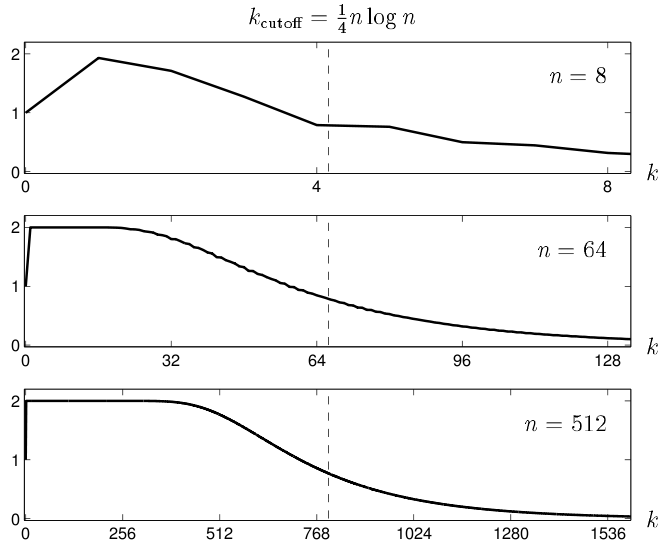
['width:800px']
Pseudospectra and
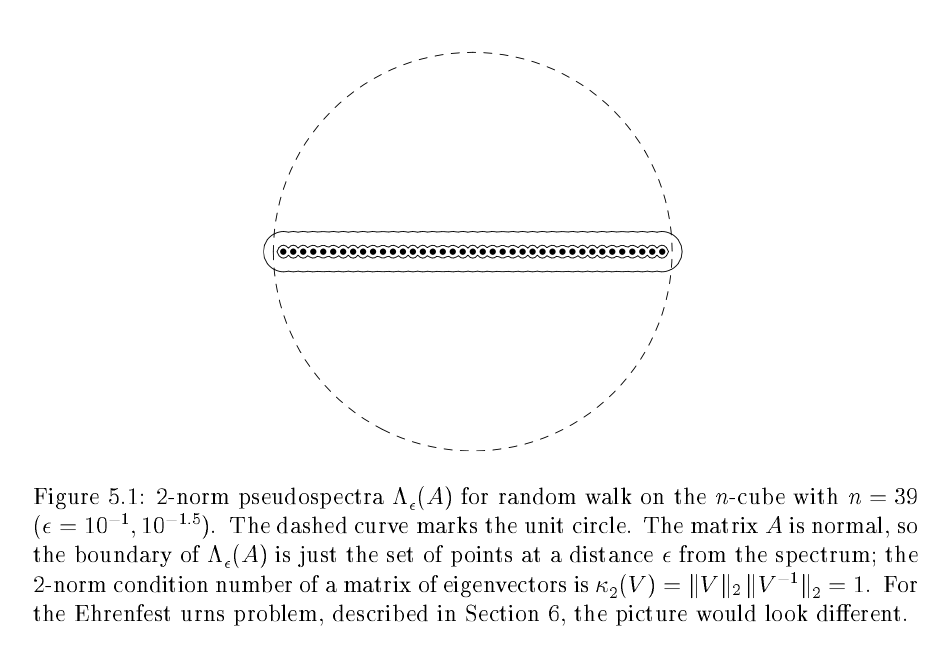
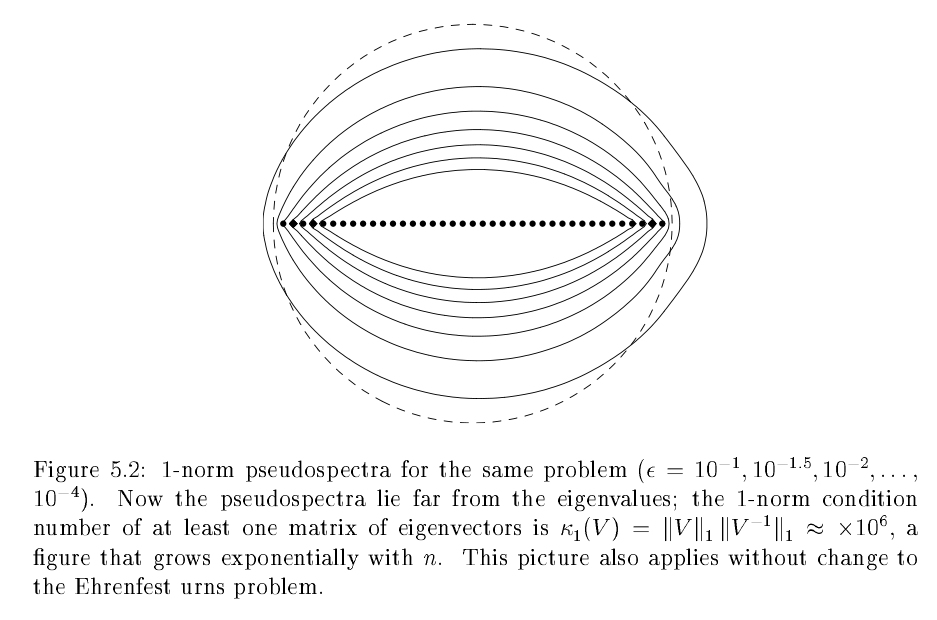
Not all matrices have critical cutoffs, drunks on a lattice for example have a smooth transition. It is generally believed that the multiplicity of the 2nd largest eigenvalue or the size of a critical in the pseudospectra are the cause.
Riffle Shuffles
A deck of n cards is cut into two portions according to a binomial distribution; thus the chance that cards are cut off is for . The two packets are then riffled together in such a way that cards drop from the left or right heaps with probability proportional to the number of cards in each heap.

Riffle critical cutoff
This describes a Markov chain on the permutations of with dimension . Thus there are approximately rows in this matrix. It is possible to prove however that the cutoff is:
This is done by reducing the problem to a (much) smaller state space, where one only considers the number of rising sequences in a permutation. For example, the arrangement has two rising sequences and interleaved together. Since rising sequences do not intersect each arrangement of a deck of cards is the determined uniquely by the union of the rising sequences.
Critical cutoff
Shuffles vs randomness
- 1, 1.000
- 2, 1.000
- 3, 1.000
- 4, 1.000
- 5, 0.924
- 6, 0.624
- 7, 0.312
- 8, 0.161
- 9, 0.083
- 10, 0.04
The first few and any subsequent shuffle after the 7th or 8th
do not bring you closer to a "random" deck.
Shuffle Pseudospectra
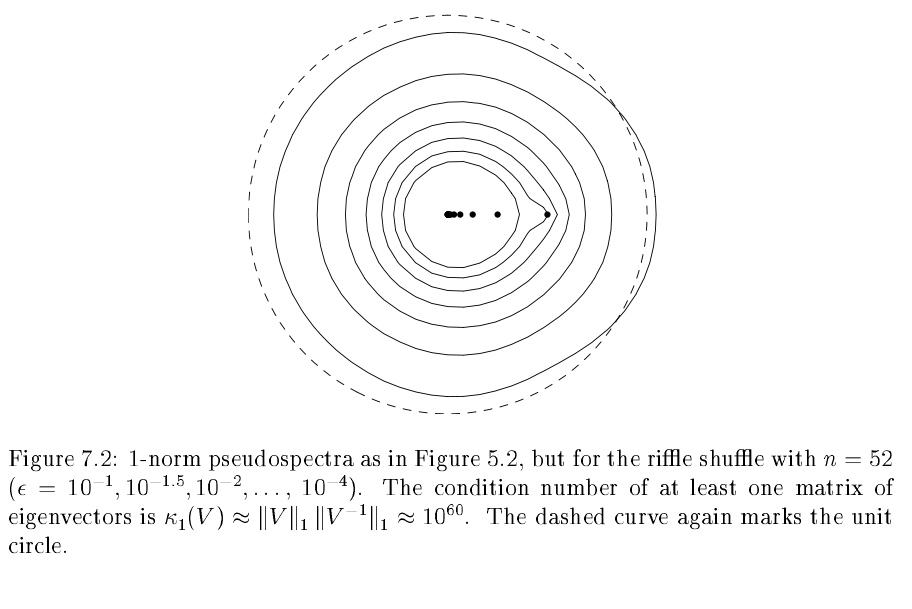
Shuffle Cutoff
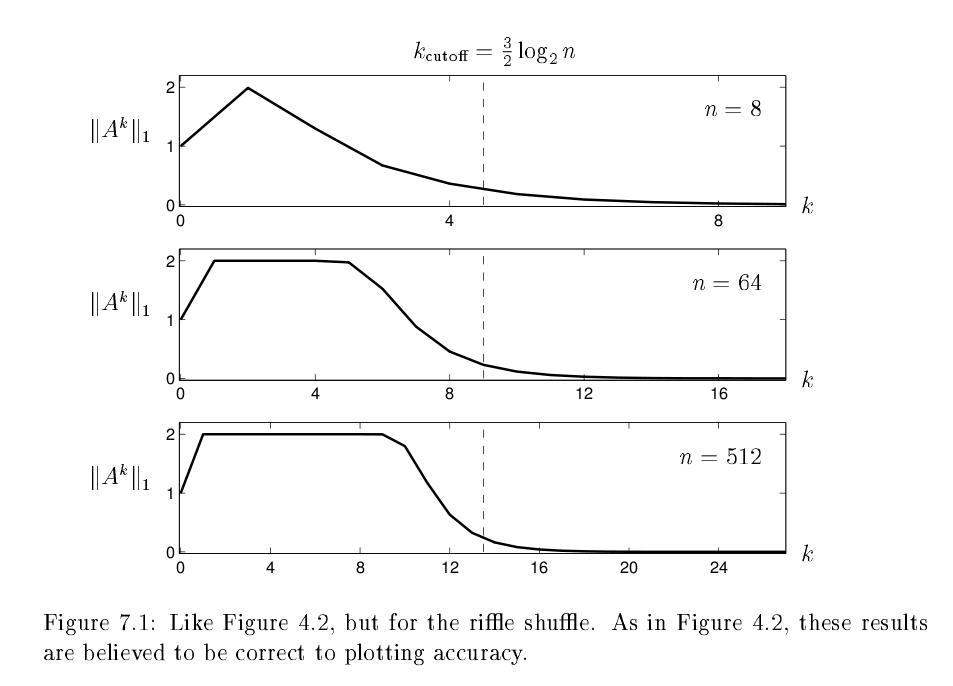
Limits
What happens when ?
Weak convergence at and
norm convergence at :