Irrelevant Topics VIII

in Physics

Travis Hoppe
(deck source)

Topics:

Quines

Price of Anarchy

Zeta Function Regularization

Quines

What is a function?

A function takes input

and produces output

What is a program?

print "Hello World"

A function takes input (code)

and produces output

Hello World

A program is a function!

Fixed points

Function points where the input is identical to the output

Can a program have a fixed point?

Fixed point programs are quines

It's not as simple as you think...

print 'Hello world'
> Hello world

print 'print \'Hello world\''
> print 'Hello world'

print 'print \'print \'Hello world\'\''
> print 'print \'Hello world\''

...

No cheating!

Some languages allow for the trivial case of empty code

No reading the code from the file

Python quine

def quine(source):
    quote = '"'*3
    print source + '(' + quote + source + quote + ')'

quine("""def quine(source):
    quote = '"'*3
    print source + '(' + quote + source + quote + ')'

quine""")

> def quine(source):
    quote = '"'*3
    print source + '(' + quote + source + quote + ')'

quine("""def quine(source):
    quote = '"'*3
    print source + '(' + quote + source + quote + ')'

quine""")

Create a function, that when called, outputs the input and
the function scaffolding

Python quine+

Once built, we can add any arbitrary code into the quine!

def quine(source):
    quote = '"'*3
x = 1
y = 2**4
    print source + '(' + quote + source + quote + ')'

quine("""def quine(source):
    quote = '"'*3
x = 1
y = 2**4
    print source + '(' + quote + source + quote + ')'

quine""")

Are quines always possible?

Quine variants

Error-quines, Iterative-quines & Multi-quines

Error-quines

Programs that fail, but the error message is valid code
(which happens to be the original source!)

Highly version and even system specific

Iter-quines

Chain of quines: output is fed back in times

Not fixed points, but cycles:

Multi-quines

Chain of quines: output of one language is fed into another

Not fixed points, but cycles of different functions:

Price of Anarchy

Nash Equilibrium

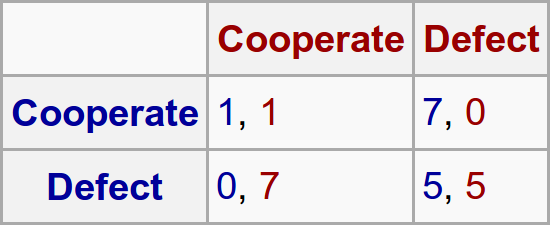
Prisoners dilemma, Nash Equilibrium is (D,D)

What is stable isn't always best

What is optimal?

Usually implies minimization of a global utility

May not be fair

May only be possible with outside help

The price of anarchy

The ratio of utilitarian to egalitarian,
or best global average to the most fair

Braess' Paradox

No shortcut

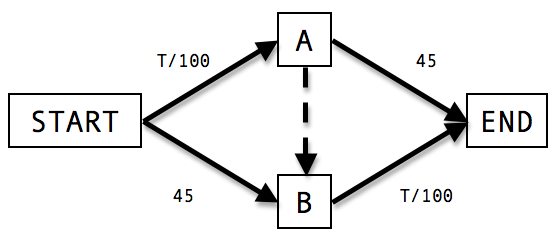
With 4000 drivers and no shortcut average time is 65 minutes
Drivers spread out evenly on both routes
This is a Nash equilibrium.

Braess' Paradox

With shortcut

With 4000 drivers and the shortcut average time is 80 minutes
Drivers only take route top/bottom
This is a Nash equilibrium.

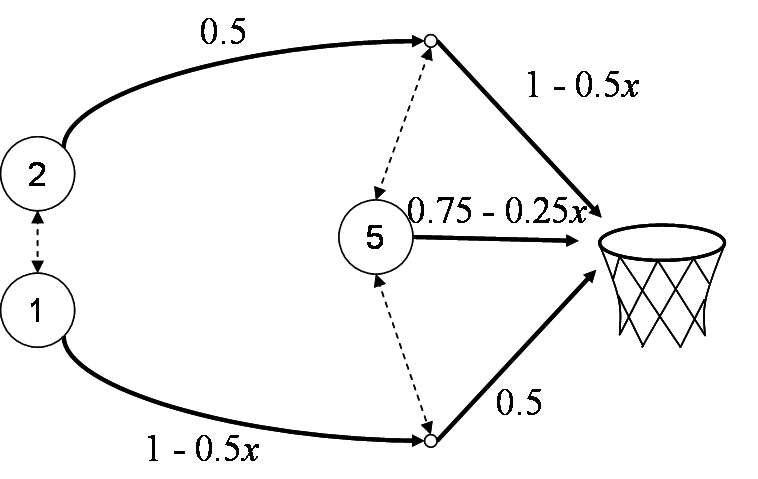
Example: Basketball

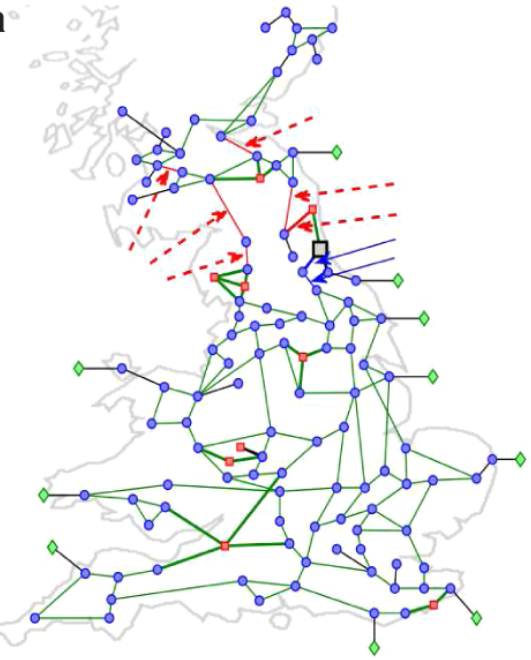
Example: Power Grids

Zeta Function Regularization

Grandi's series

Loosen the idea of a sum

Cesaro sum

Take the limit of the arithmetic means

Thus Grandi's series is "Cesaro" summable to 1/2

Abel summation

Take the series

Consider the power series

If it converges in , then take limit

Alternating series

Partial sums visit every natural integer!

Cauchy product of two Grandi series

Not Cesaro summable, but an Abel summation gives 1/4

Can also be solved with

Euler Transforms

Borel summations

Main event

-1/12

Zeta function

For this is the Riemann zeta function (super important)

Zeta function regularization

Let be our series and (let's pretend)
that everything will be OK at

...let's pretend that everything
will be OK at ?

has a simple pole at

and only converges for

It can be analytically continued

onto the complex plane

is not Abel summable, but it can be zeta regularized when we analytically continue onto the complex plane

It is a shadow of the original function, but it is finite...

Casmir Effect

Consider the expectation value of the zero-point energy
for all standing waves of an E&M field in a cavity

This sum clearly diverges ...
for mortals

Casmir Effect in detail

Casmir Effect in detail

The force scales as
This is real and can be measured!

One more to wrap it up

This has a radius of convergence of 1/2 hence it is not convergent at 1. However there is a unique analytic continuation onto the complex plane with 1/2 deleted.

Thanks, you.