Virial
Coefficients
of Charged Protein Solutions
NIH, NIDDK, LBG
Travis Hoppe, Allen Minton, Di Wu
(deck source)
Main Idea
Predict from structural informationagainst
pH Dependence
Concentration
Charge anisotropy
intra-protein interactions

Human serum albumin, Ovalbumin, Lysozyme, Bovine Serum Albumin respectively.
How do we model the interaction between proteins on a larger scale? Can we predict aggregates?
Mixtures
Phase separations lead to sudden fundamental changes in liquid structure and local density.


This is usually really important.
Basic Science
Match experimental data with results
of computational models.
Classify common protein solution behavior
from coarse-grained models.
Predict behavior of mutations and unknown solutions.
Virial Coefficients
An equation of state expanded in powers of density is the pairwise interaction of two moleculesis the pairwise interaction of three molecules
...
Necessary first step for a verifiable model.
Virial Coefficients
For rotationally invariant molecules
(where is the pairwise interaction energy)but in general...
Virial Coefficients
Why work with this expansion?How do you model a
protein?
Need an expression for the interaction energy
This is not the free energy, but the enthalpy
Important terms:
- Volume exclusion
- Electrostatics
- Non-specific interactions (London/dispersion forces)
How do you model a
protein?
Second-order effects?
- Non spherical geometries
- Polarization
- Internal conformational energies
- Solvent effects
Must decide if this approximation is valid for the system.
modeling the
Excluded Volume
(it's easy!)
Hard spheres
overlap energy is either or
modeling the
Electrostatics
(not so easy)
Electrostatic field
Coulomb's Law (point charge)
Correction for dielectrics?
What about the solvent?
Yukawa Potential
First order approximation to screening effects.
Charge strength decays exponentially due to ions.
Poisson Boltzmann
Describes the electrostatic interaction between a charge distribution and an ionic solution.
Can be linearized and solved on a computer efficiently.
Splits space into regions of discrete .
The Process

Start with the crystallized PDB Structure (HSA)
Adaptive Poisson-Boltzmann Solver
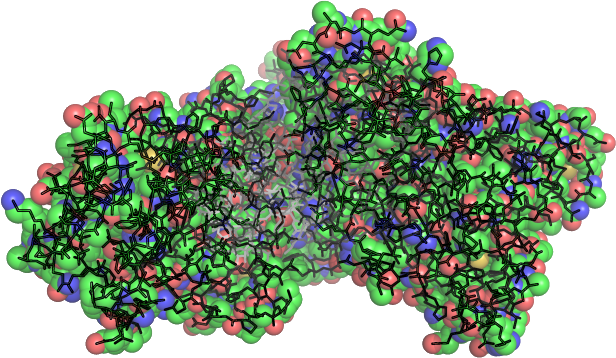
Typically (in the absence of ions)
,
The Process
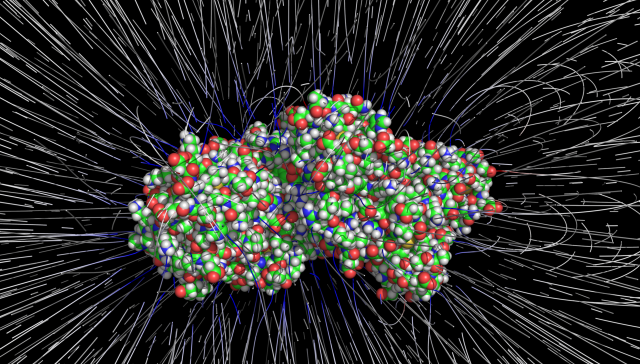
Electrostatic field
The Process
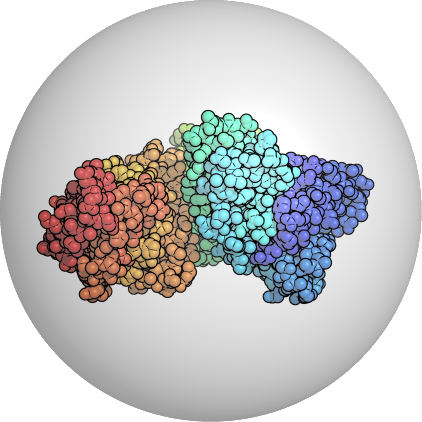
Determine a region of excluded volume.
The Process
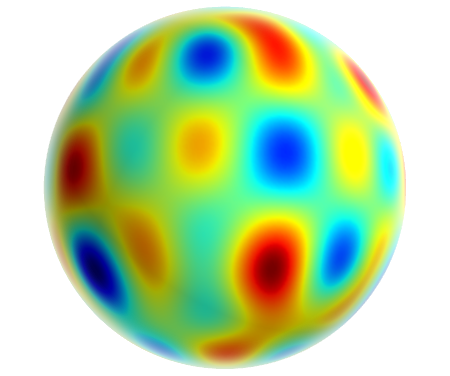
Spherical Harmonic decomposition for large distances.
The Process
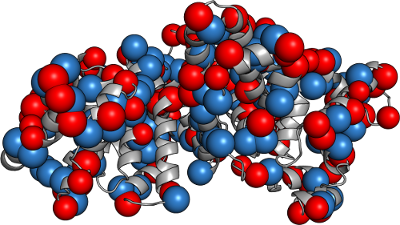
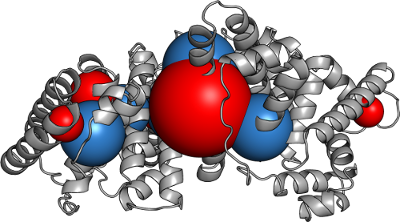
Best fit macrocharges to replicate the field.
This works

Protein Caricatures
Good approximation of the near field, poor up close.
Captures the anisotropic field
especially near the isoelectric point.
Macrocharge approximations make for reasonable
models of large protein solutions.
So Far...
Excluded volume for modeled as a hard sphere.
Representation of the protein electrostatics
in an ionic solution for a given pH.
What's next?
(work in progress)
Remember this?
Our charge distributions are not isotropic anymore,
we must to compute this:
Sampling woes
There are many pairwise orientations.
Blind sampling may miss specific interactions.
Need to know at different if we want to scale the model.
Density of states
counts the number of ways
we can get a particular energy,
efficiently calculate with Wang-Landau.
Calculate the non-ideality of a protein molecule after including both the excluded volume and electrostatics.
Predict the second-virial coefficient as a function of pH values, protein concentrations, binary mixtures, and salt concentrations.
If experimental results agree, use the model in higher-order simulations to predict phase behavior via Gibb's ensembles.
That would be really neat.
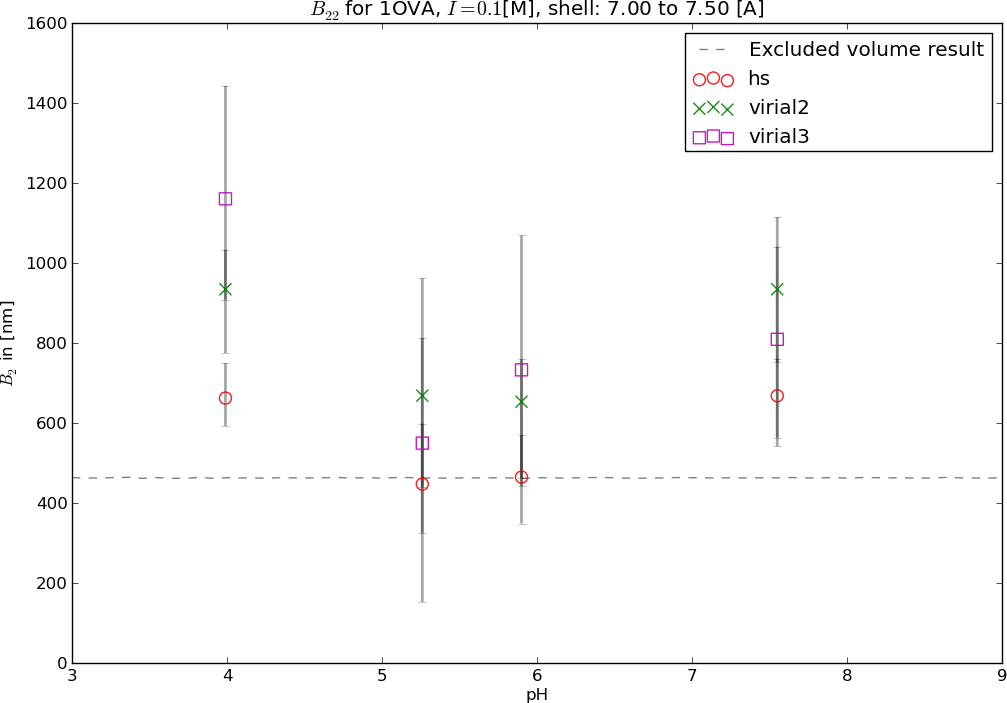
Results for Ovalbumin

Future work
Large scale Monte-Carlo simulation using macrocharges.

results for square-well potentials shown
Thanks, you.
How were these slides made?
Math Rendering:
JavaScript : reveal.js
Markdown : Daring Fireball
Markdown to HTML: md2reveal.py
How does it work?
A text-based human-readable markup.
SVG equations , and links!
The code for this particular slide looks like this:
## How does it work?
A *text-based* human-readable markup.
Equation rendering is simple $e^{i \pi} = -1$.
and [links](http://thoppe.github.io/)!
The code for this _particular slide_ looks like this: