Topological Considerations
of the
Wang-Landau
sampling algorithm
Motivation
What connection is there between the
moveset, energy landscape & selection rules
and the convergence and accuracy
of sampling algorithms?
Can we do better?
Metropolis Sampling
Boltzmann vs. Wang-Landau
Each samples a specific distribution.
WL Modification
Original formulation
Reduce modification factor when is "flat".
Reduction rate,
Use original formulation for initial sampling.Switch to when smaller than original formulation.
Wang-Landau advantages:
Wang-Landau gotchas:
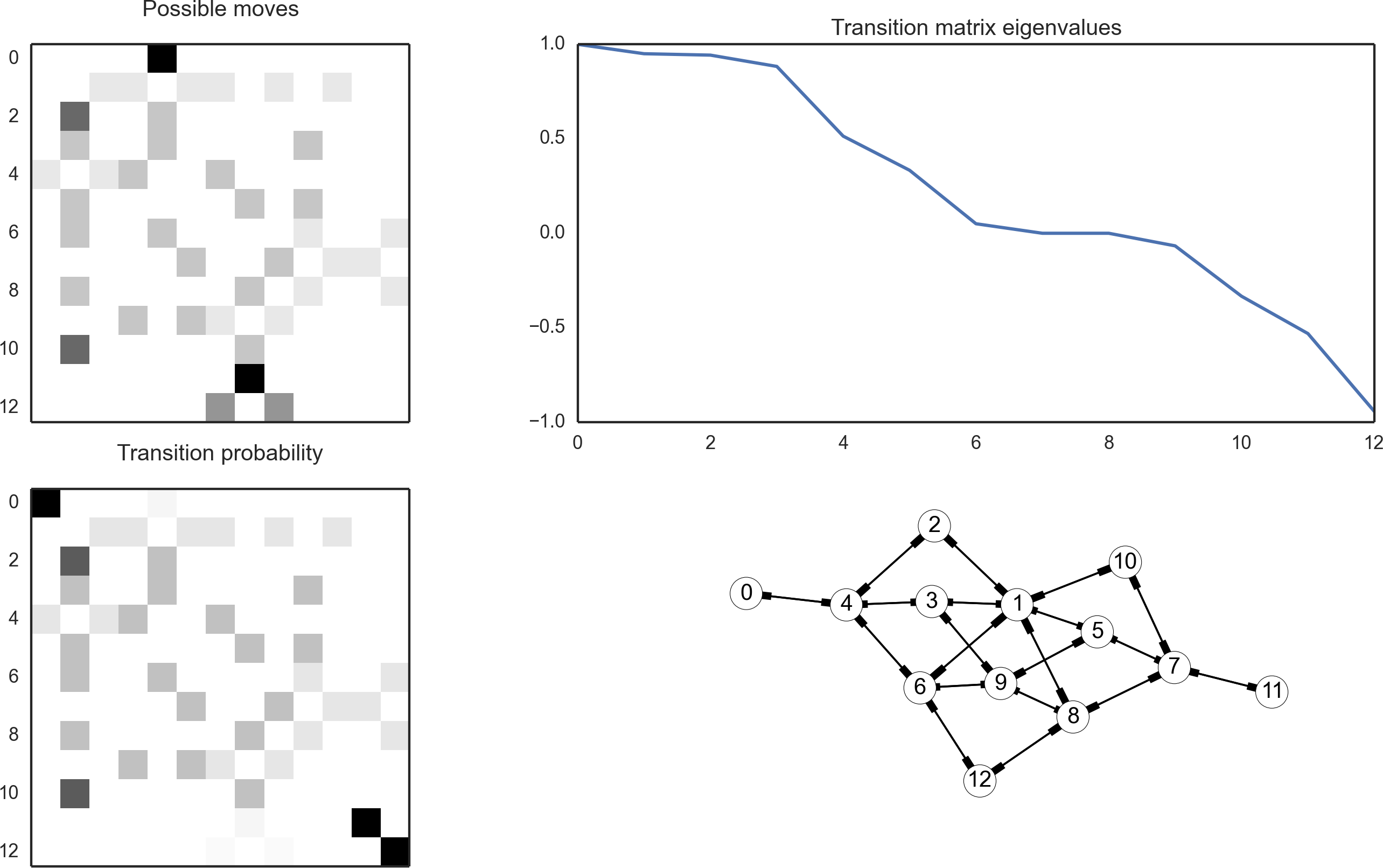
"Topology" of states?
Let be the set of microstates of the system.In order to process any sampling algorithm, one needs
- An acceptance function, , .
- A microstate weighting function, , .
- A moveset function, .
The moveset defines a directed graph with vertices , and edges . A sampling algorithm follows a random walk on given by .
Example: Ising/Potts model
A network of spin sites that interact via
where the sum is over all adjacent sites (typically a lattice).
Single spin flips define a moveset.
Other possible moves: double flips,
inversions, Glauber-type.
Ising model "topology"
With fixed , how does WL perform?
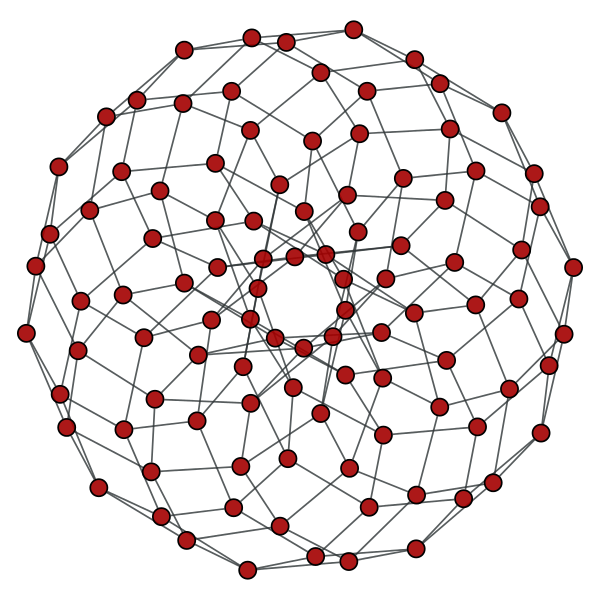
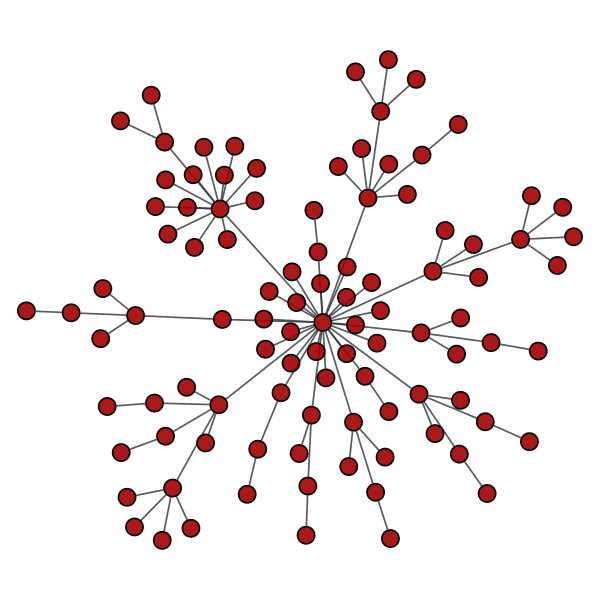

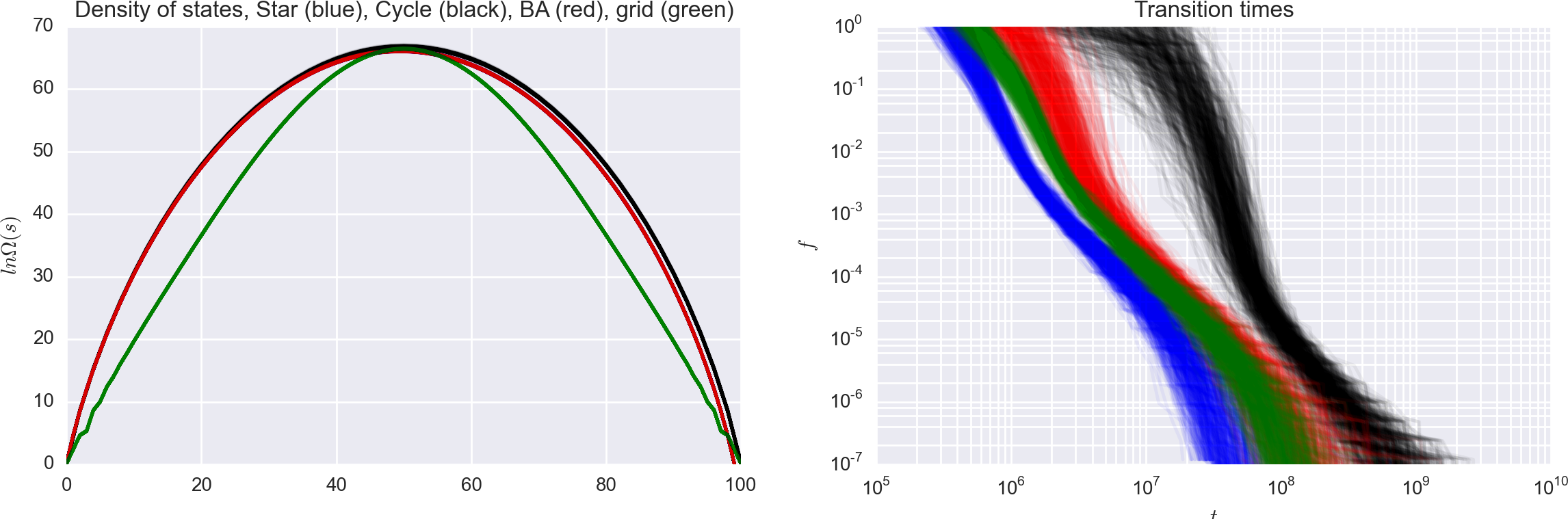
What about graphs that follow other
degree distributions and correlations?
Is there a difference?
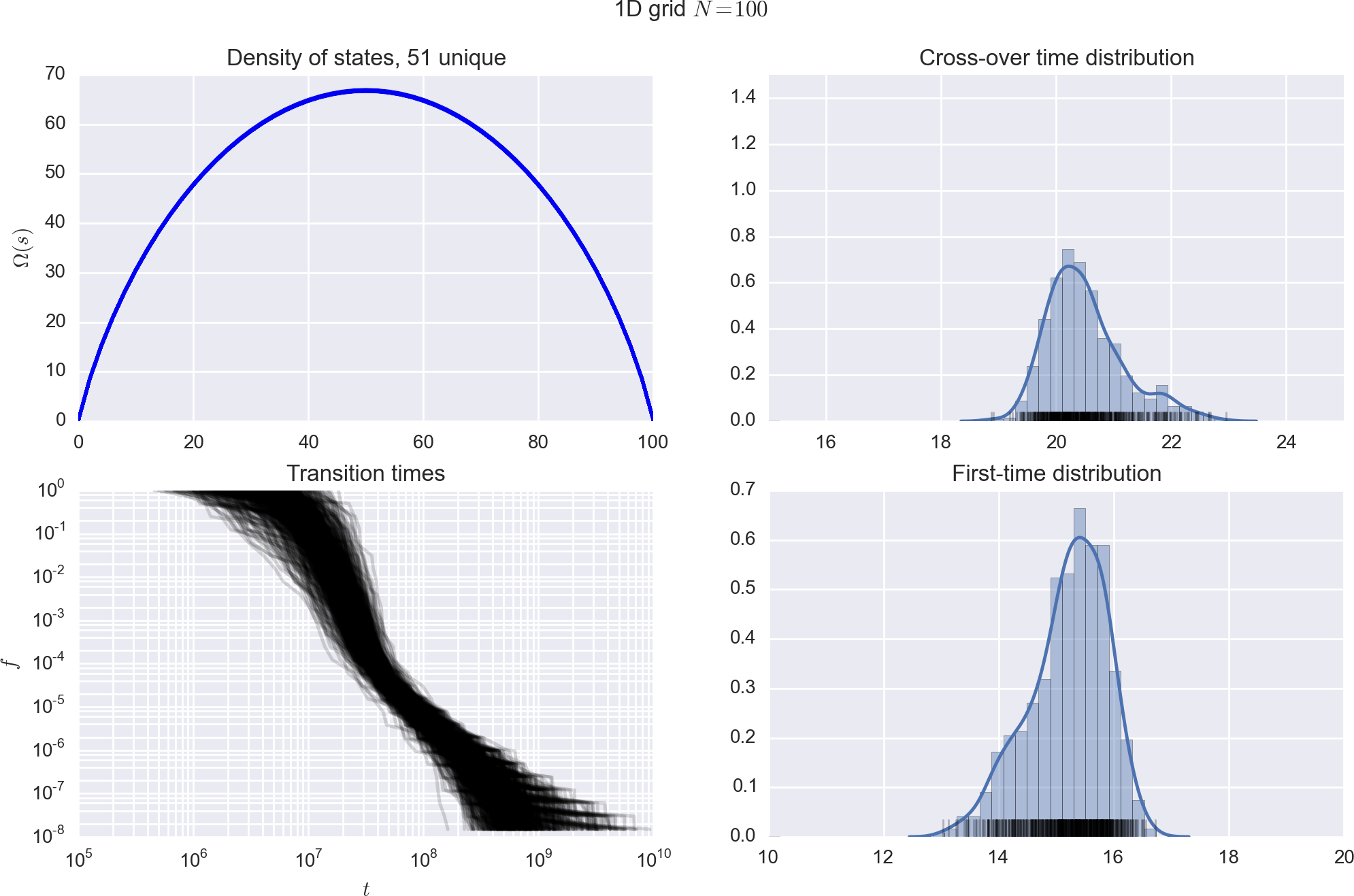

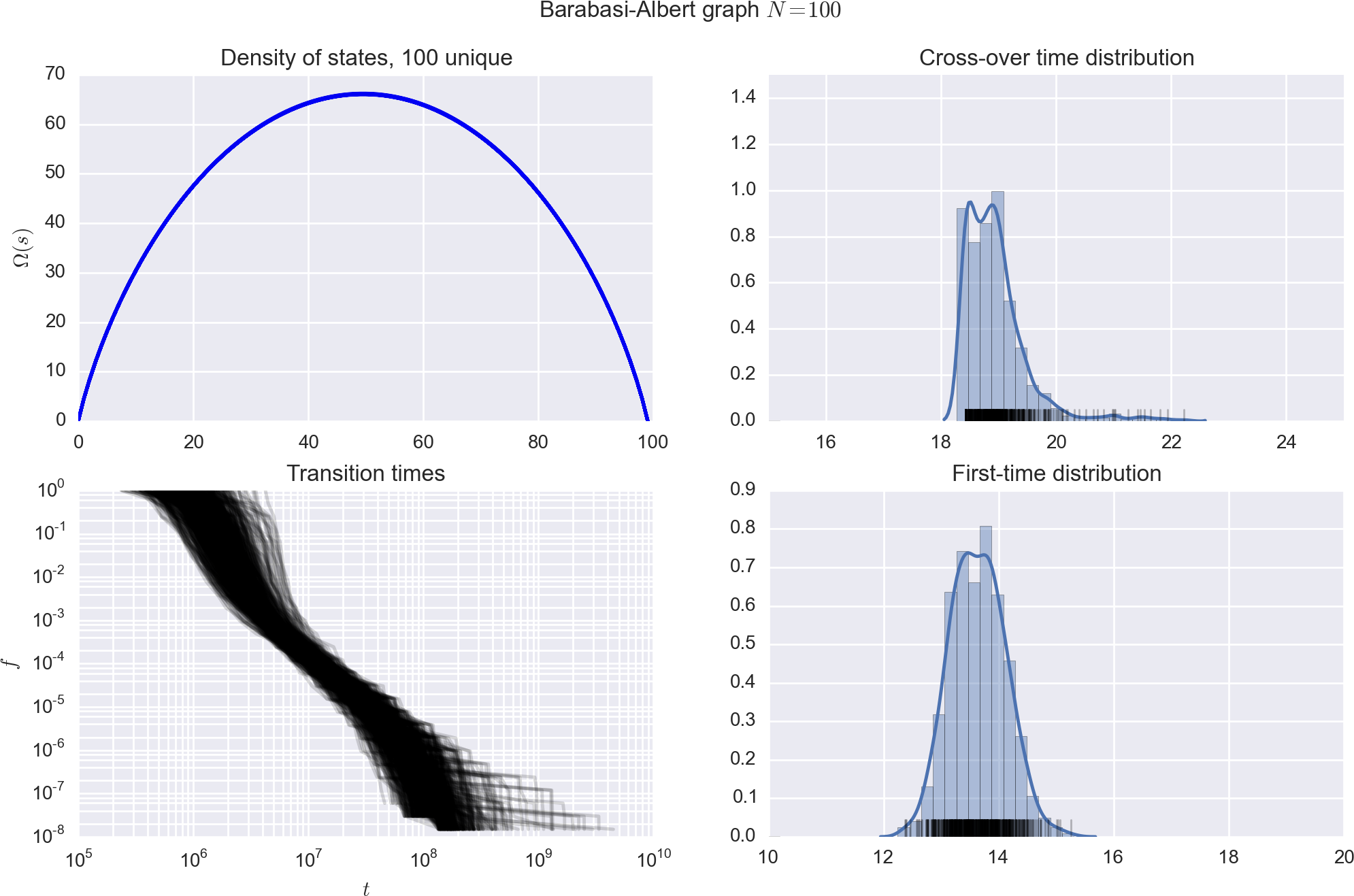
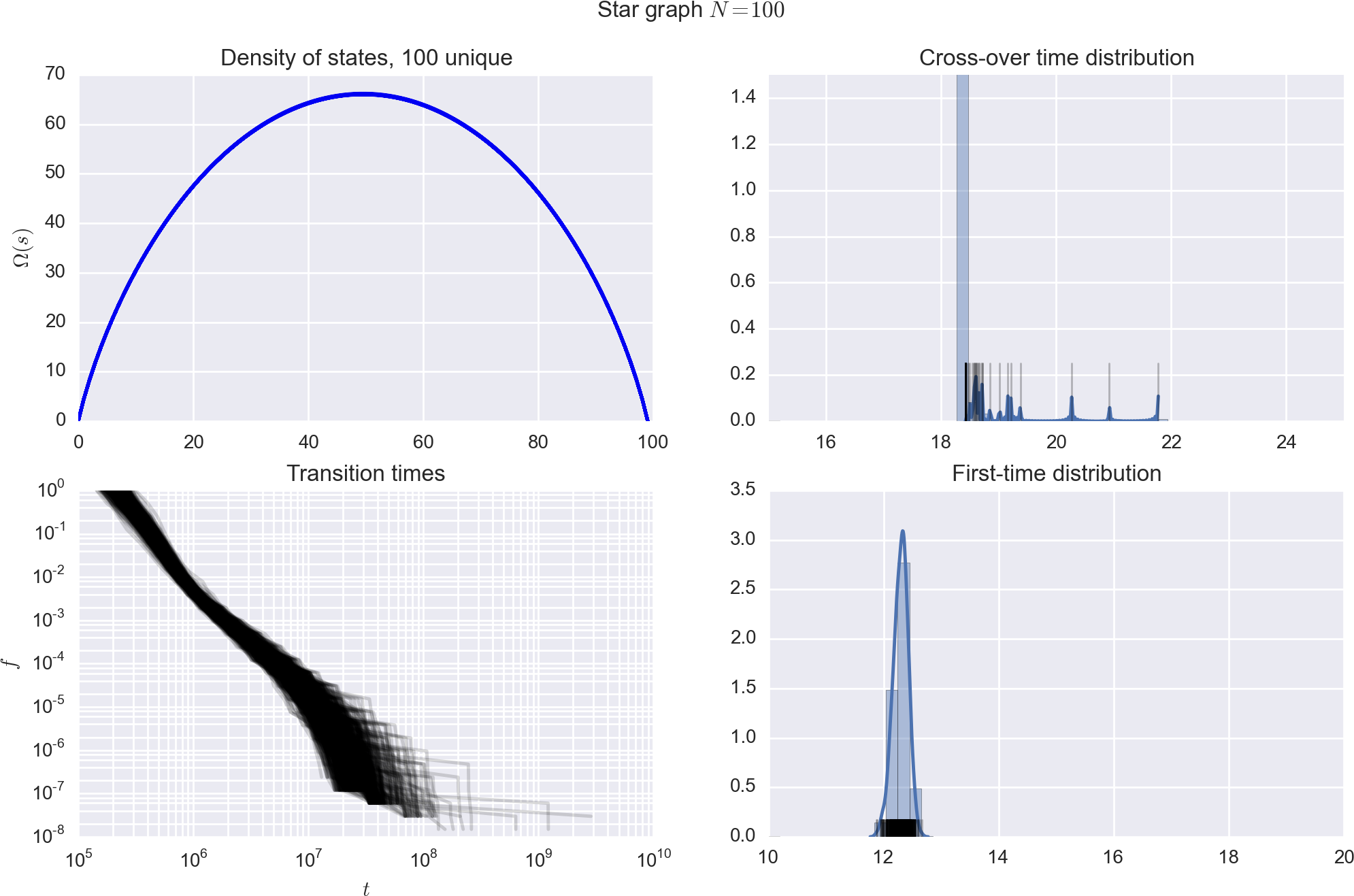
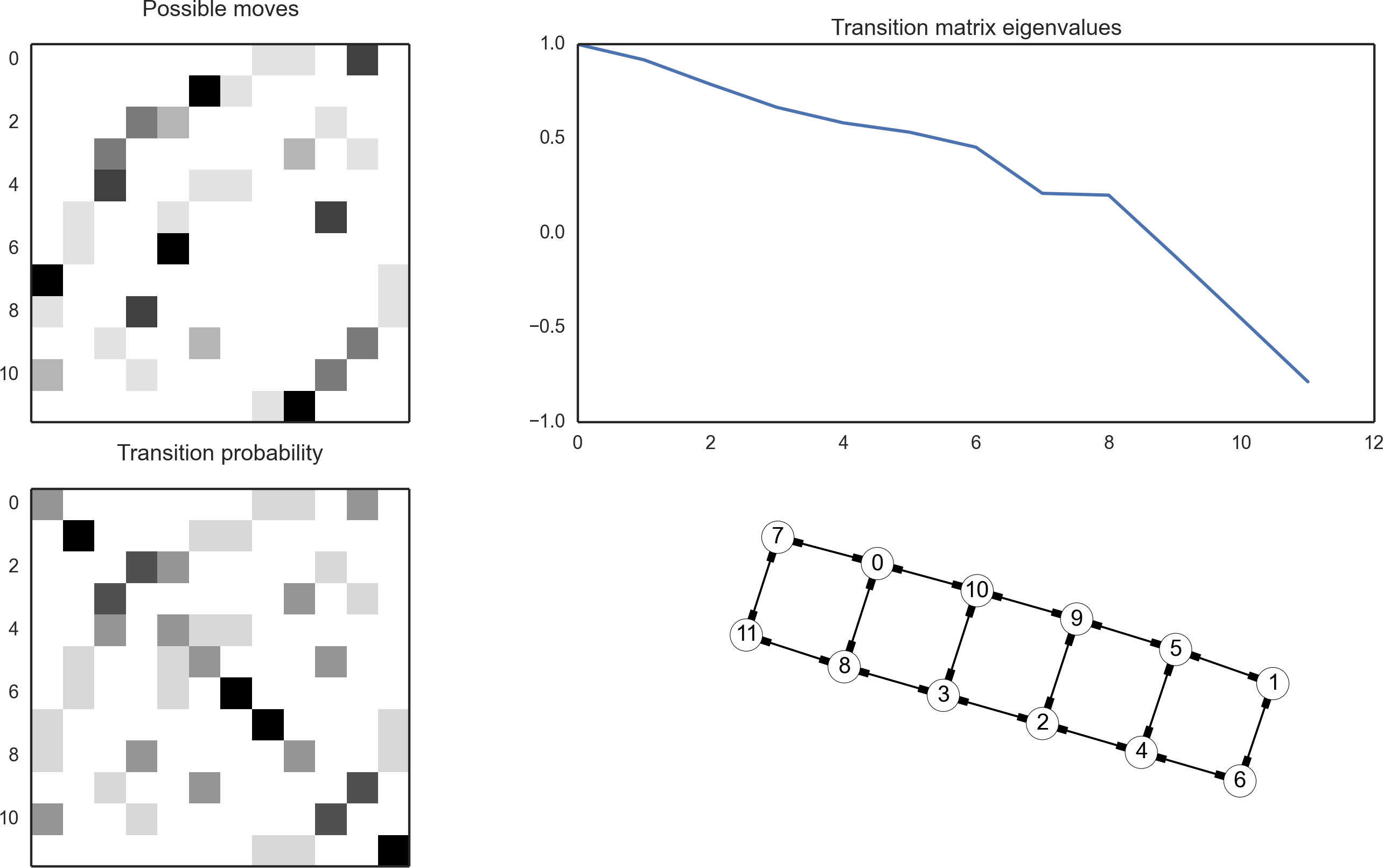
Star graph,

1D periodic chain, cycle graph,

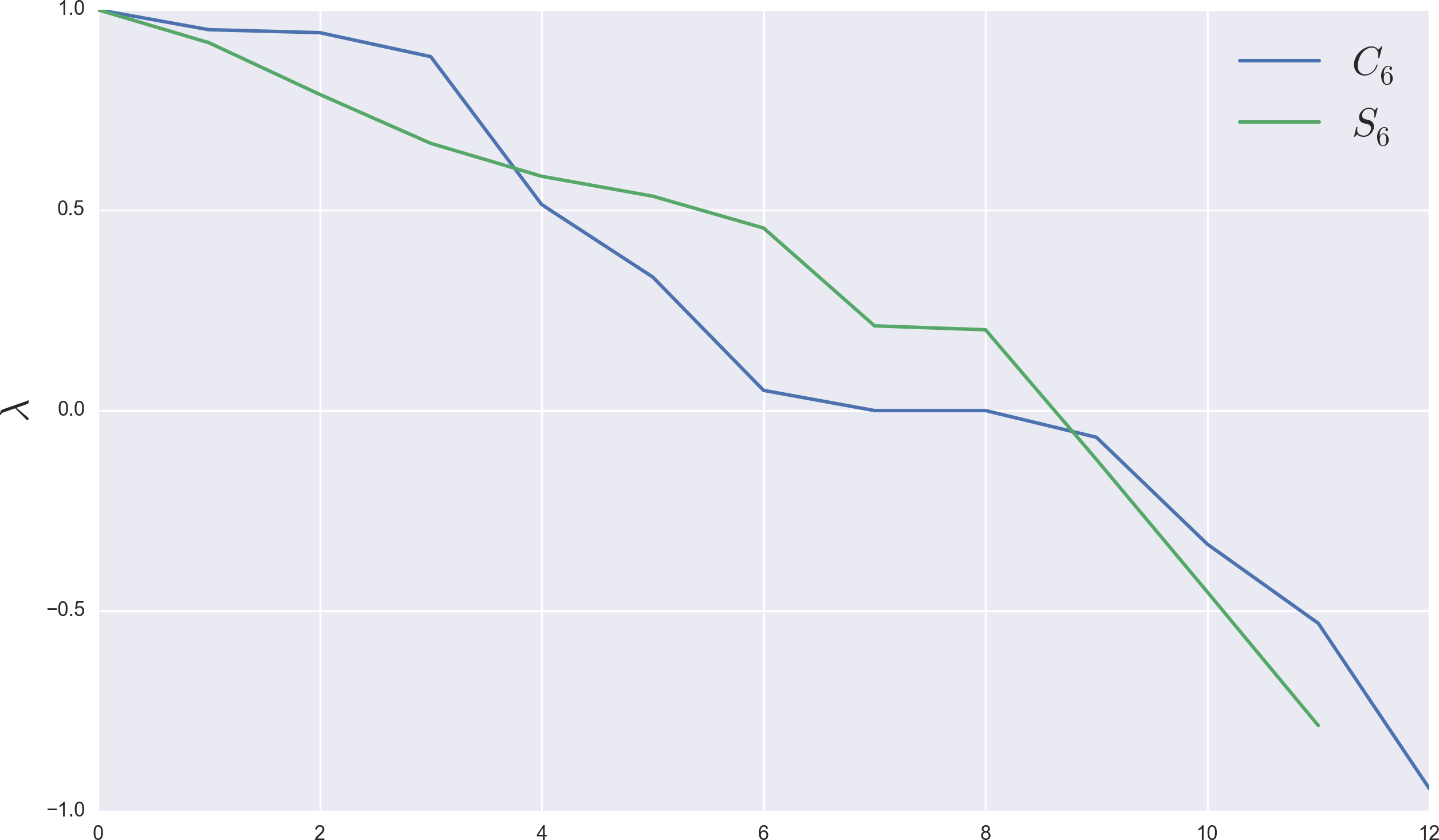
Relative convergence times
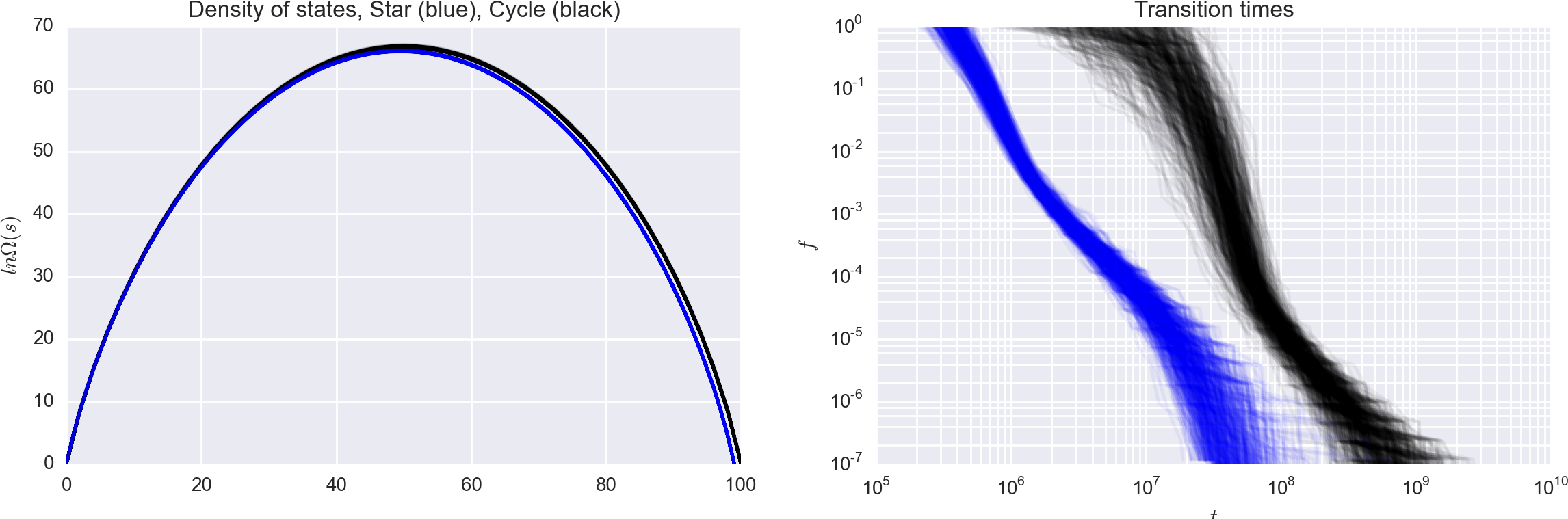
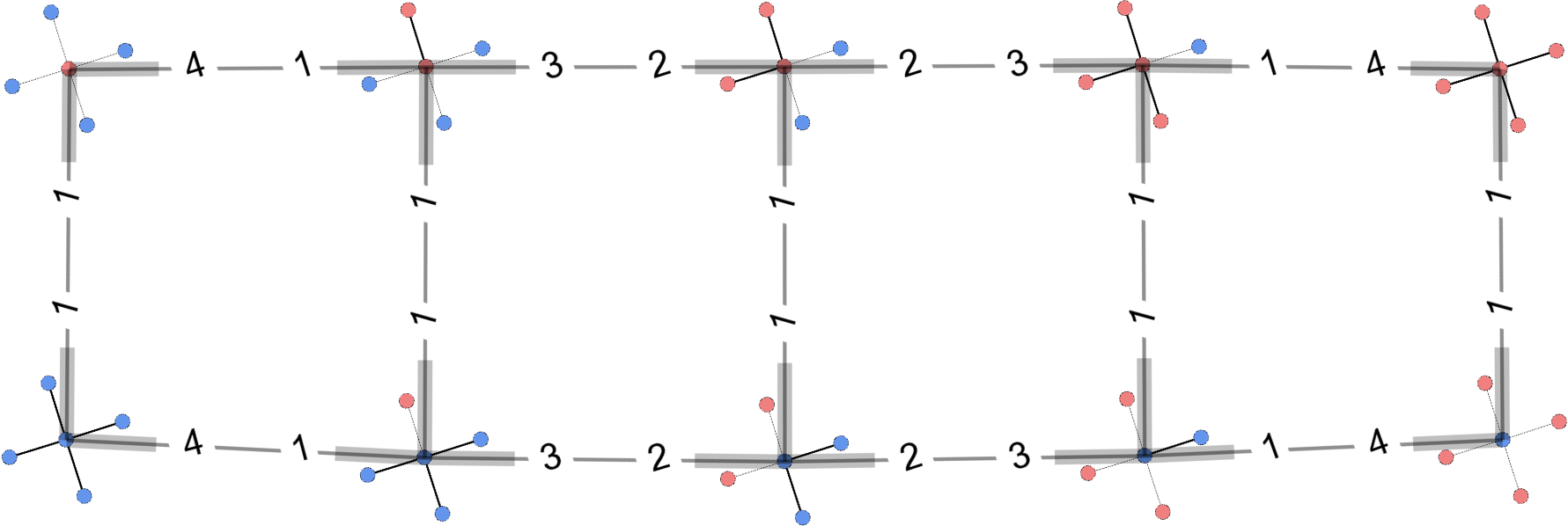
Isomorphic reduction
Reduce microstate spaceto mesostate space defined by spin isomorphs.
Group the microstates into isomorphically
different arrangements of spins;
Star topology,

Cycle topology,
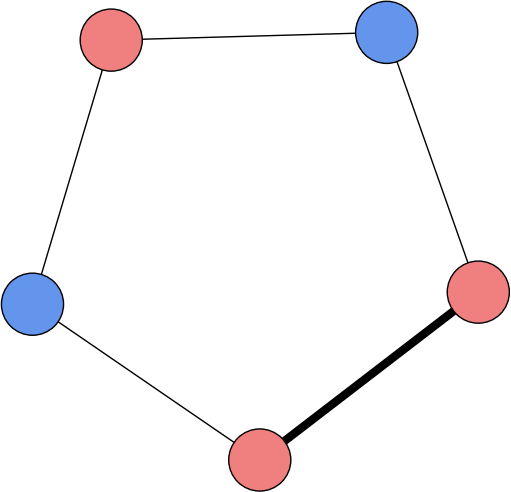
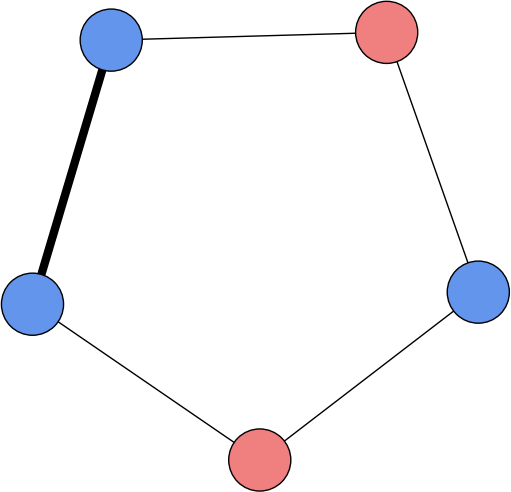
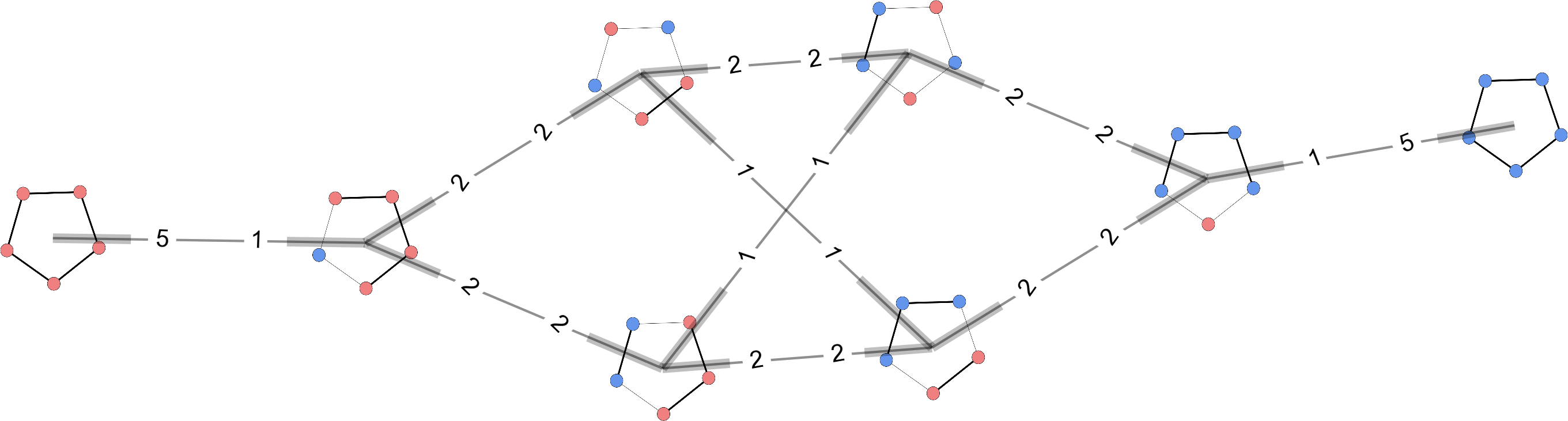
Cycle topology,
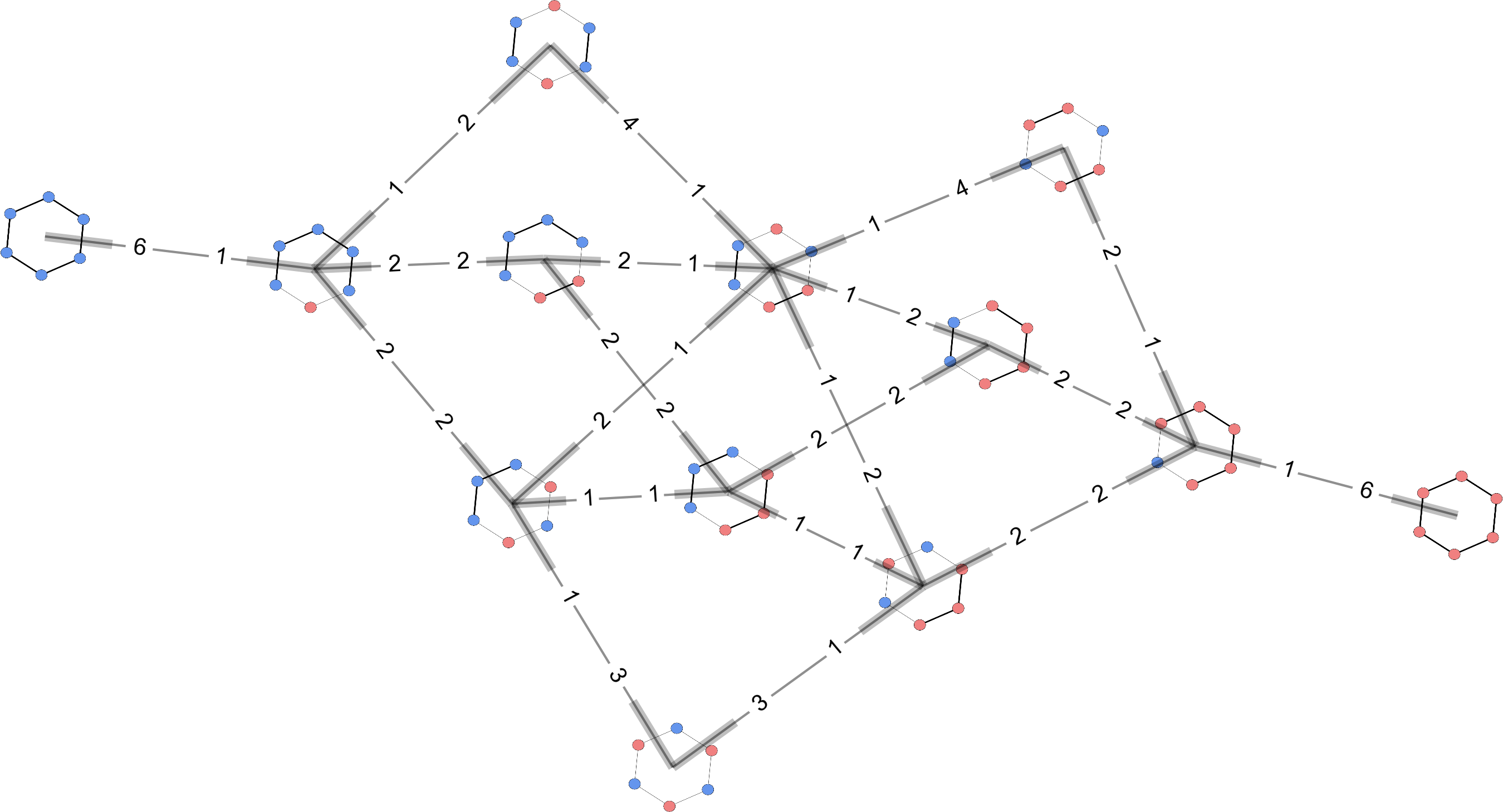

Topology matters!
Two systems with similar and DOS,yet widely different convergence times.
Same moves (single-spin flips), different moveset graphs.
Stars gives rise to "ladder"-type moveset graphs,
cycles are more complicated.
What can we change?
Measures of accuracy
Minimize spectrum of converged WL walks.
Minimize "round-trip" time between two extermal states.
Spectrum analysis
Once WL is fully converged, it is Markovian with aneigenvalue spectrum
Moveset optimization
We can optimize a new move by minimizing and weighting the new move relative to the old ones.
Possible new moves, inversions, -spin flips,
bridges, and "cheats".
This changes the edges in the moveset graph.
Assume that optimized moves will carry over during
the non-Markovian phase of the algorithm.
Cheater moves,
allow all possible isomorphs to connect,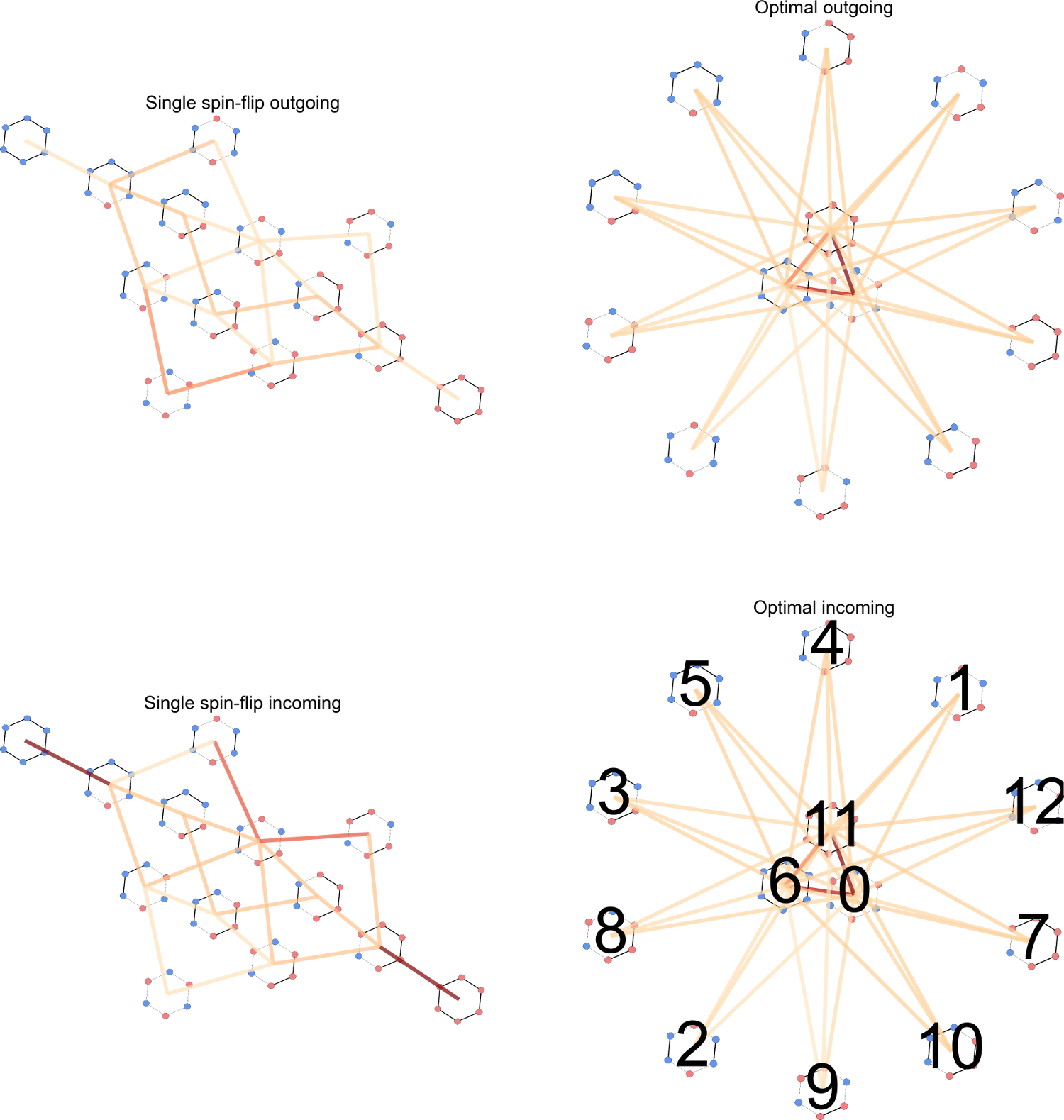
Cheater moves,
allow all possible isomorphs to connect,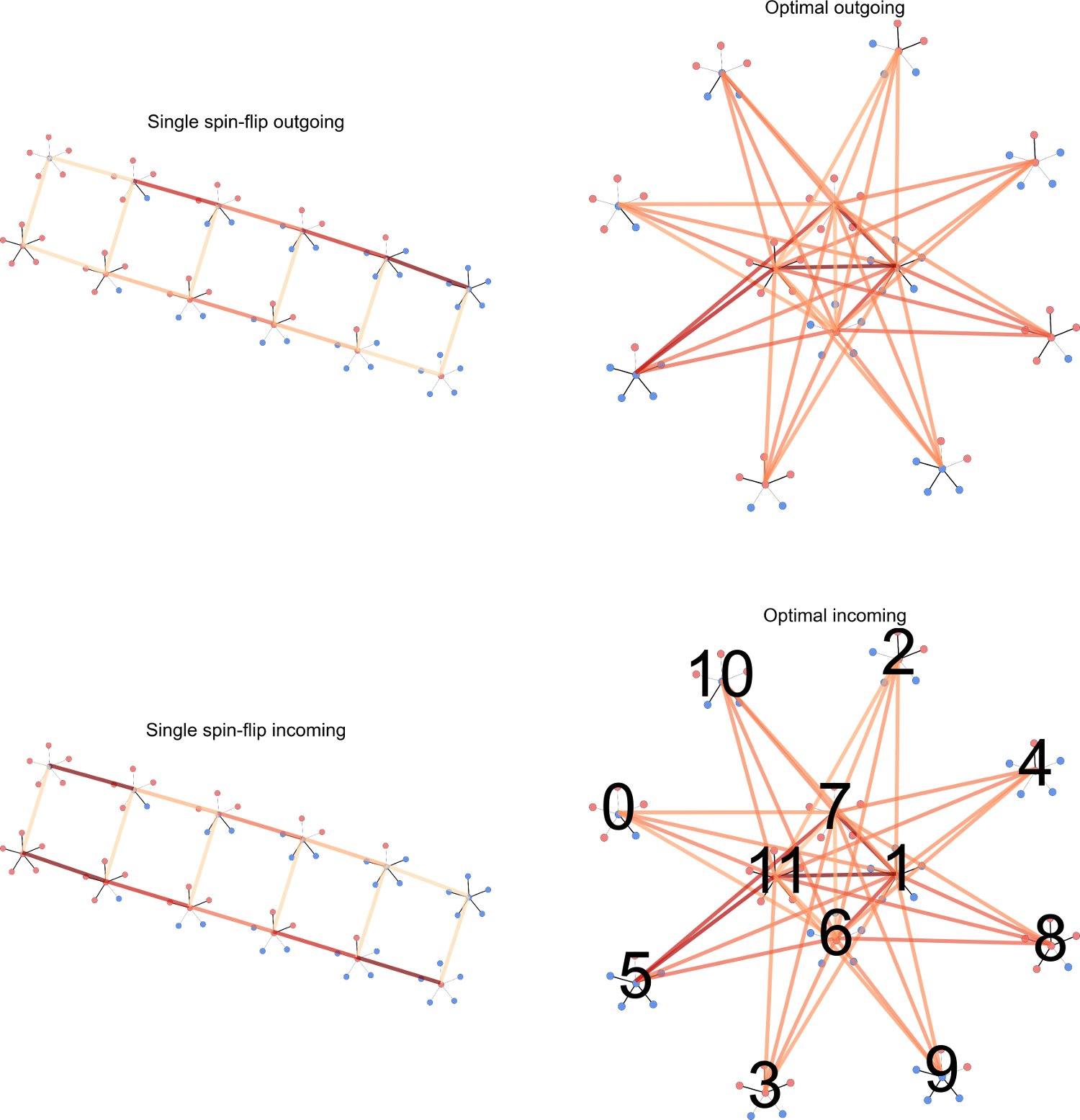
Weight optimization
Fix the moveset, now try to optimize the weights.
This leads to non-flat histograms.
Trebst sampling (minimize round-trip times)
Isochronal sampling (minimize and match RT times)
Trebst sampling
Labels flow of walkers from extermal states,
.
Expand steady-state current to first order,
Assume that the weights are slowly varying in energy,
Energy optimized weights for
Optimize over isomorphs?
Absorbing Markov Chains
mean/variance of absorbance times
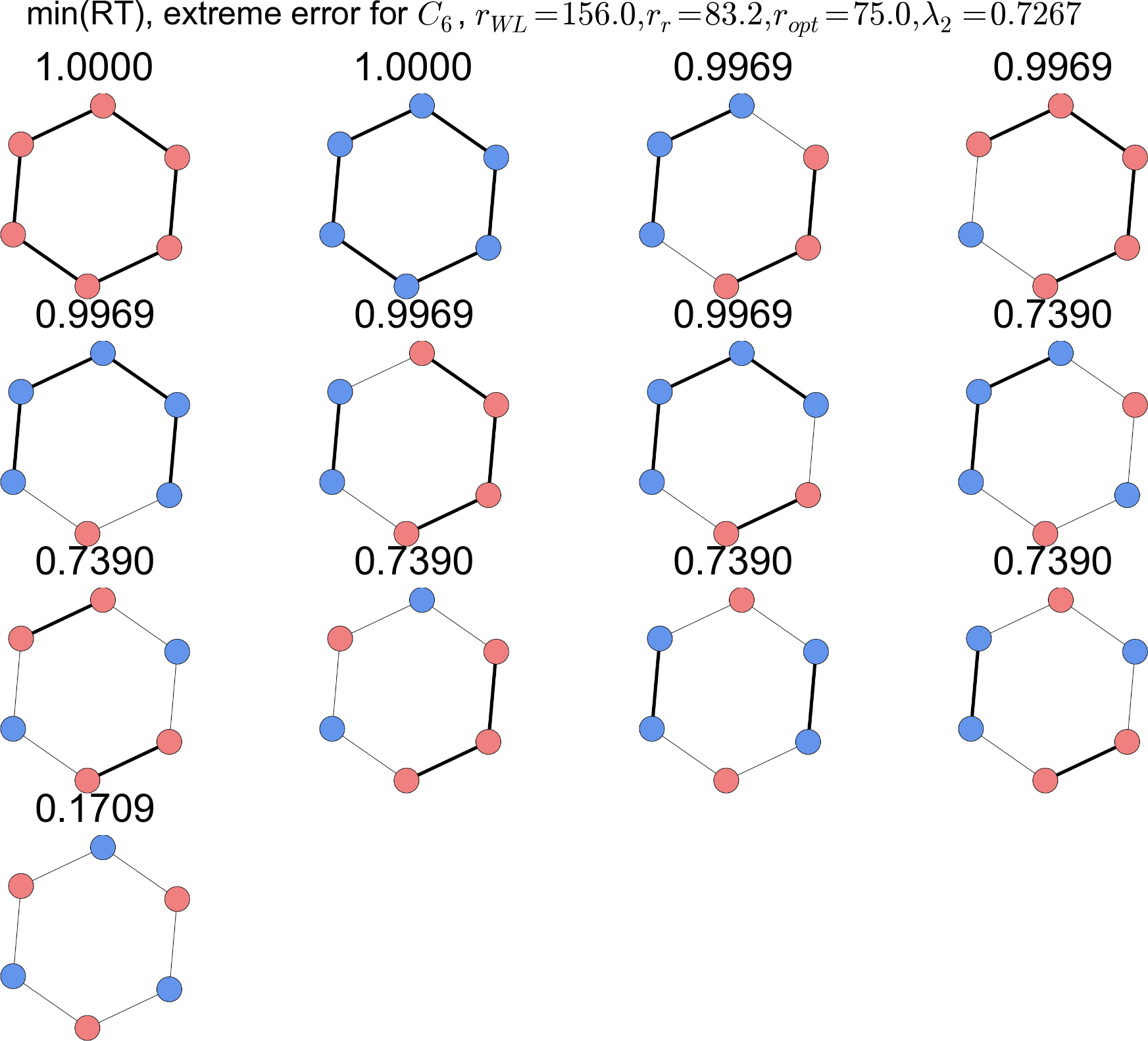
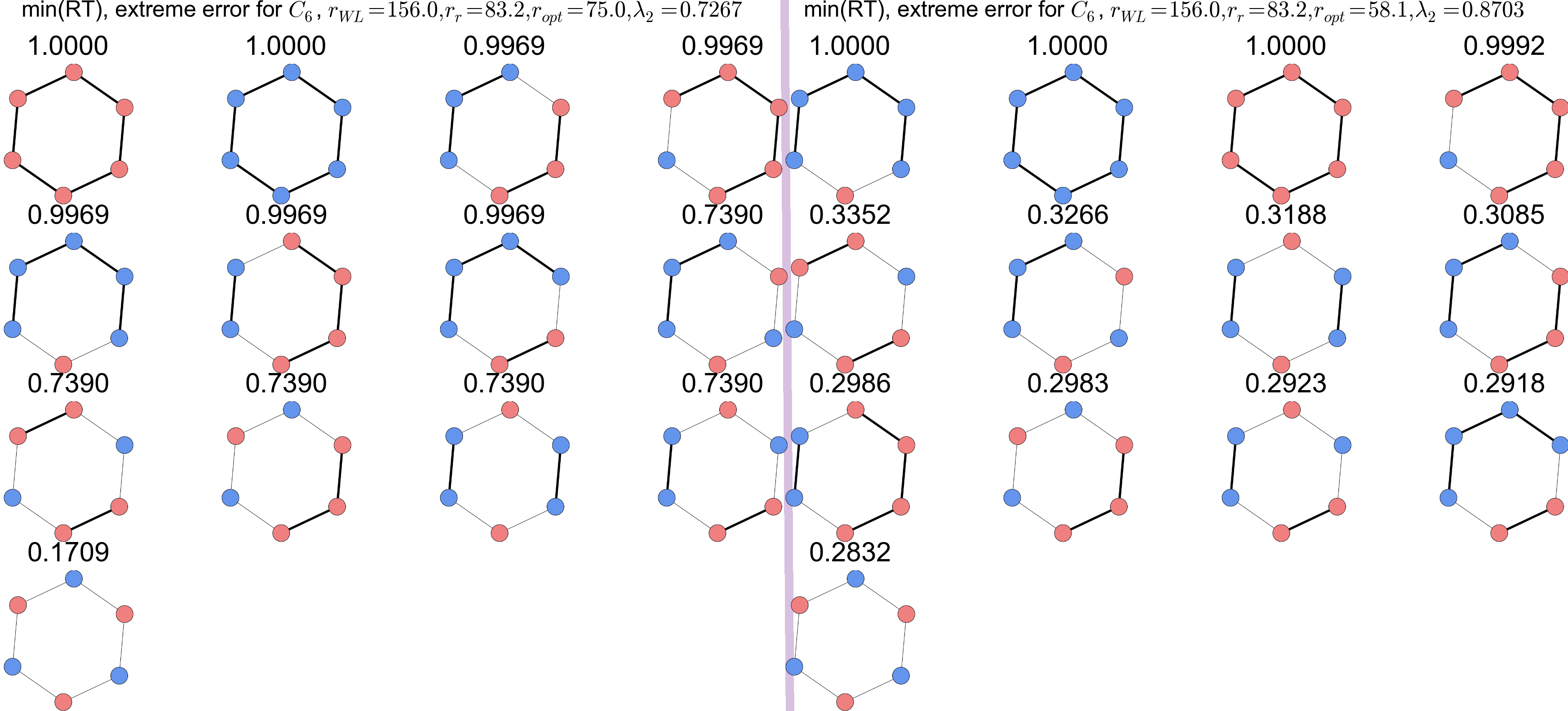
Isomorph optimized weights,
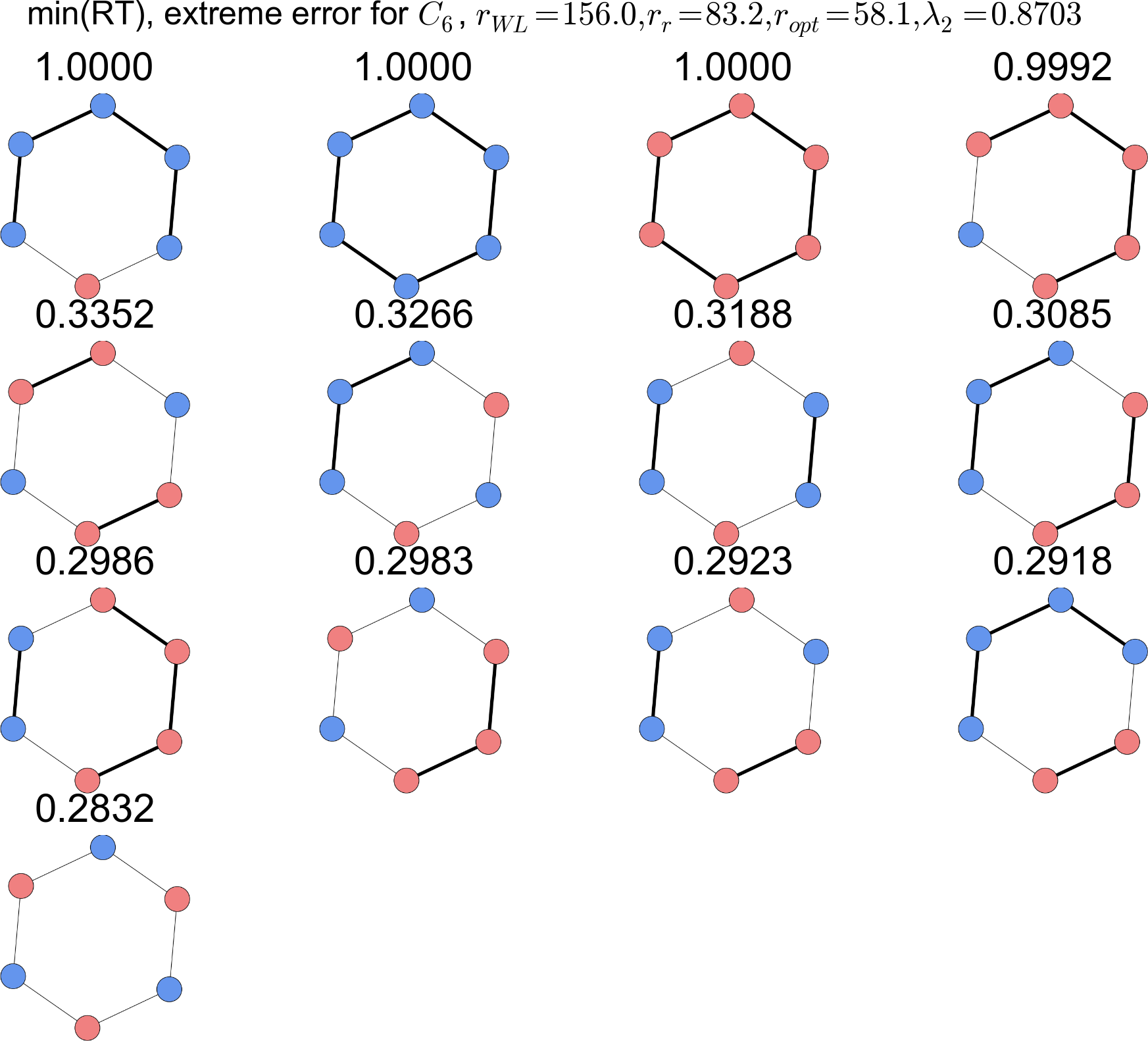
Energy vs. Isomorph (macro vs. meso)
What's next?
WL, Trebst, and Isochronal weights
are not necessarily optimal.
Minimize not just round-trip between
all states, not just extermal states?
Consider not just mean round-trip times,
but higher moments (e.g. variance, skew)?
Quantify the sampling difficultly
by the moveset topology?
Conclusions
There is room for improvement in the optimal moveset,
small systems provide insight to larger state space.
Trebst sampling is an improvment over flat histograms,
but assumes smooth DOS.
Sampling at energy macrostates is coarse,
it possibly could be improved with better macrostate fidelity.