Irrelevant Topics I
in Physics
Topics:
Dissipative Lagrangians
Physics
Supershapes
Geometry
Random Walks On Regular Lattices
Physics
Dissipative Lagrangians
Forbidden couplings in phase space
Normally we work with "nice" potentials
However, there are some systems that depend on the path taken.
The simplest is the damped harmonic oscillator
Forbidden couplings in phase space
One way to formalize this system was done by Morse and Feshbach
When we apply Euler's equations of motion
We get the following differential equations
This system conserves energy!
For every bit lost by the original damped harmonic oscillator,
it's gained by it's mirror.
Lest you think that dissipative Lagrangians can only
be constructed with a "dual", one can also use
The exponential multiplier does not induce any extraneous solutions.
Euler's equations of motion would produce the
original differential equation.
Supershapes
almost squaring the circle
Not so super
Circles
Ellipses
Superellipses
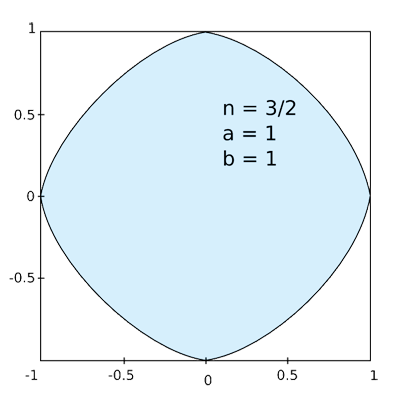
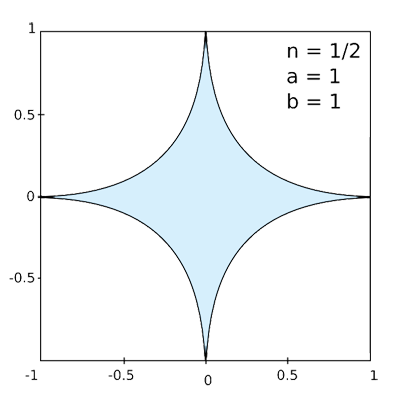
The last one is cheerfully named the squircle.
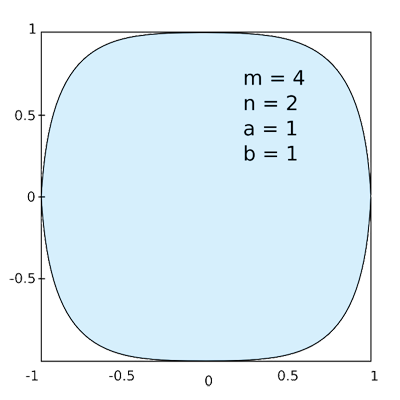
Superellipses
Random Walks on Regular Lattices
or the best dimension to get drunk
A random walk on a lattice takes an integer step with
equal probability in one of the possible directions.
A walk is recurrent, if the probability of returning to the
starting point approaches one as the number of steps go to infinity.
One-Dimension
Let be the number of possible ways from starting at iand ending at j in exactly n moves. From the binomial theorem:
With some approximations:
Thus a random walk is recurrent in 1D.
Two-Dimensions
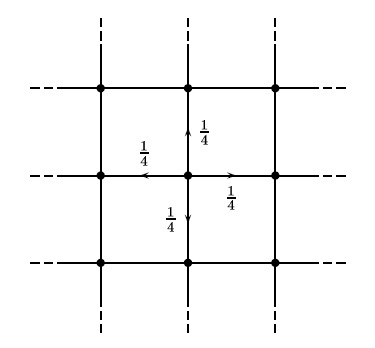
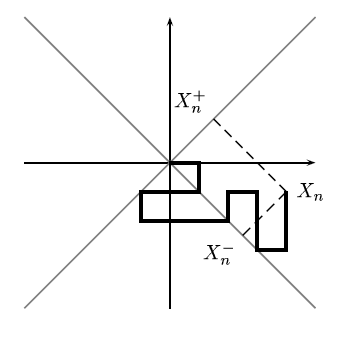
Xn+ and Xn- are simple symmetric independent random walks.
Thus a random walk is recurrent in 2D
Three-Dimensions
Thus a random walk in 3D is not recurrent!
Do not get drunk in 3D!
If you lose your keys in space,
odds are you will never find them again...
Thankfully, Earth has a 2D periodic surface!