Irrelevant Topics VII

in Physics

Topics:

Benford's Law

one is not the loneliest number

History

Simon Newcomb (1881) noticed the wear on logarithmic tables was not uniform. Suggested that the a priori assumption of the most significant digit distribution was not uniform. Frank Benford (1938), physicist, tested the hypothesis over many datasets.

What is Benford's law?

Benford's Law (in base 10)

Benford's Law (in other bases)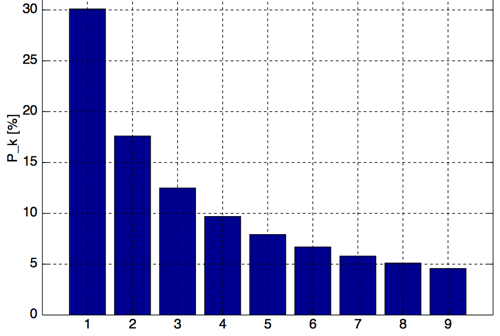

Examples

Benford's original paper took data from many disparate sources

Rivers (335)
Population (3259)
Physical constants (104)
Newspapers (100)
Specific Heat of Materials (1389)
Pressure (703)
Molecular Weights (1800)
Drainage (159)
Atomic Weights (91)
and (5000)
Readers Digest (308)
(900)
Death Rates (418)
Street Addresses (342)
Black body radiation (1165)

Distribution of Distributions

Benford's law applies not only to scale-invariant data, but also to numbers chosen from a variety of different sources.

As the number of variables increases, the density function approaches that of the above logarithmic distribution.

It was rigorously demonstrated that the "distribution of distributions" given by random samples taken from a variety of different distributions is, in fact, Benford's law.

Why might this be so?

Exponential growth

Numbers are not uniformly distributed, but the logarithms are...

Scale Invariance

If an underlying distribution exists, then it must be scale invariant. The only continuous distribution that satisfies this is logarithmic.

Mixing of Distributions

While drawing from a single Gaussian would fail, multiple Gaussians from multiple sources would follow Benford's law.

Can it fail? (yes)

Numbers that fail to span large orders of magnitude, or numbers that aren't "numbers" such as the lottery or telephone numbers.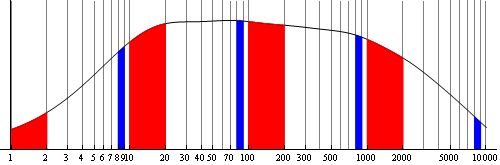

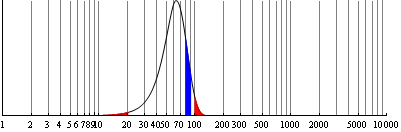
Favorite Examples

Benford's Law is now considered admissible evidence
for fraudulent claims in forensic accounting.

Some numerical distributions follow Benford's law exactly,
such as , and the Fibonacci numbers.

The 54 million real constants in Plouffe's
Inverse Symbolic Calculator database follow Benford's law.

Negative Specific Heat

getting more by pushing less

Something Reasonable

One expects that the average internal energy , of a system in contact with a thermal bath should increase with , the bath temperature.

Why might this be so? Consider

Recourse to the Virial theorem

Astronomers have experience with such systems. If the system obeys the Virial theorem with potential energy that scales as with external edge pressure and volume

Isolated gravitational fields give , and

Simple 3-level model

Assign a simple (Boltzmann) transition rate, but couple states and to different thermal baths, say and . For simplicity, disallow .

Using the Master equation, the average energy is

There is a range of values where

['height:300px']

The intuitive explanation is the creation of the barrier
of the forbidden .

Negative Conductivity

Suppose a particle moves stochastically but is driven (say by an electric field, with driving energy ) down two lanes. The particle has the following movement probabilities, where

1, for crossing lanes
x, for moving upstream
1/x, for moving downstream

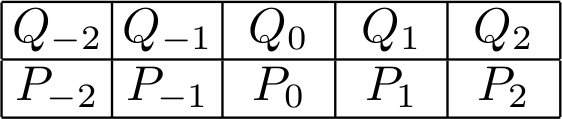
Negative Conductivity

In the uniform case, this gives a current density that is always positive

Now introduce a barrier

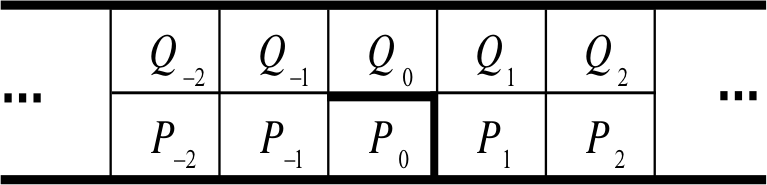
The conductivity for sufficiently large !

Real world examples

Biological membranes, different heat
coupling in the membrane and outside

Brownian noise with a driven diffusion

Negative mobility and sorting of colloidal particles

Real Computability

a waste of the number line

Preliminaries

We must understand two things first:

Computability

Cardinality

What makes a number computable?

A Turing machine is a theoretical device to manipulates symbols on a strip of tape according to a table of rules.

A Universal Turing machine (UTM) can emulate any other UTM.

A language is Turing complete if it is a UTM (e.g. python, ruby, C++, etc)

A number is computable if you can write a finite piece of code to compute any specified digit.

Computable Numbers

How can be computable if it has an infinite amount of "information"? Consider the following program

Cardinality

How do you compare sets?

We get that . How can we do that if we can't count them? We say that two sets have the same cardinality, , if we can find a bijection (i.e. a mapping from one to another)

Infinite sets

Common fields

Whole numbers
Natural Numbers
Rational numbers
Real numbers

This works for infinite sets as well (see Irr. Topics 3).
Think about vs .

...

Thus .

Cantor and aleph-naught

The smallest infinity is , but

While there are just as many fractions as integers, there are "more" real numbers than fractions! (details: if the continuum hypothesis holds ).

Uncomputable numbers

Think of all possible programs one could write (say in python), let this set be . Some of these programs run and spit out an answer in a finite amount of time and halt, some of them run forever (some programs have syntax errors and never run, give them a run time of zero).

There is a real number, called Chitin's constant, that represents the average halting probability for all programs.

is not computable. This is the Church-Turing thesis, and is directly related to Gödel's incompleteness theorems.

How big is ?

Since the programs in can be enumerated,
we must have the case that

This means that all computable real numbers
are equal in size to the whole numbers.

Which means that a random point on the
real number line is not-computable.

This implies that (almost) every number we use in physics amounts
to an infinitesimal fraction of the real number line!

The question of physics and the real number line is intimately tied to the discreteness of Nature.

If one built a machine (more powerful than Turing) that could use all of the real numbers, one could solve all of the "hard" problems easily. It would imply that .