zerozerozero
Buddhabrot-style polynomials
Standard Mandelbrot vs Buddhabrot


Math Review
🧪
Quadratic polynomials
always
have two roots
Roots can be real or complex
Always has n (possibly complex) roots
If
a
are all real, then all the roots are real
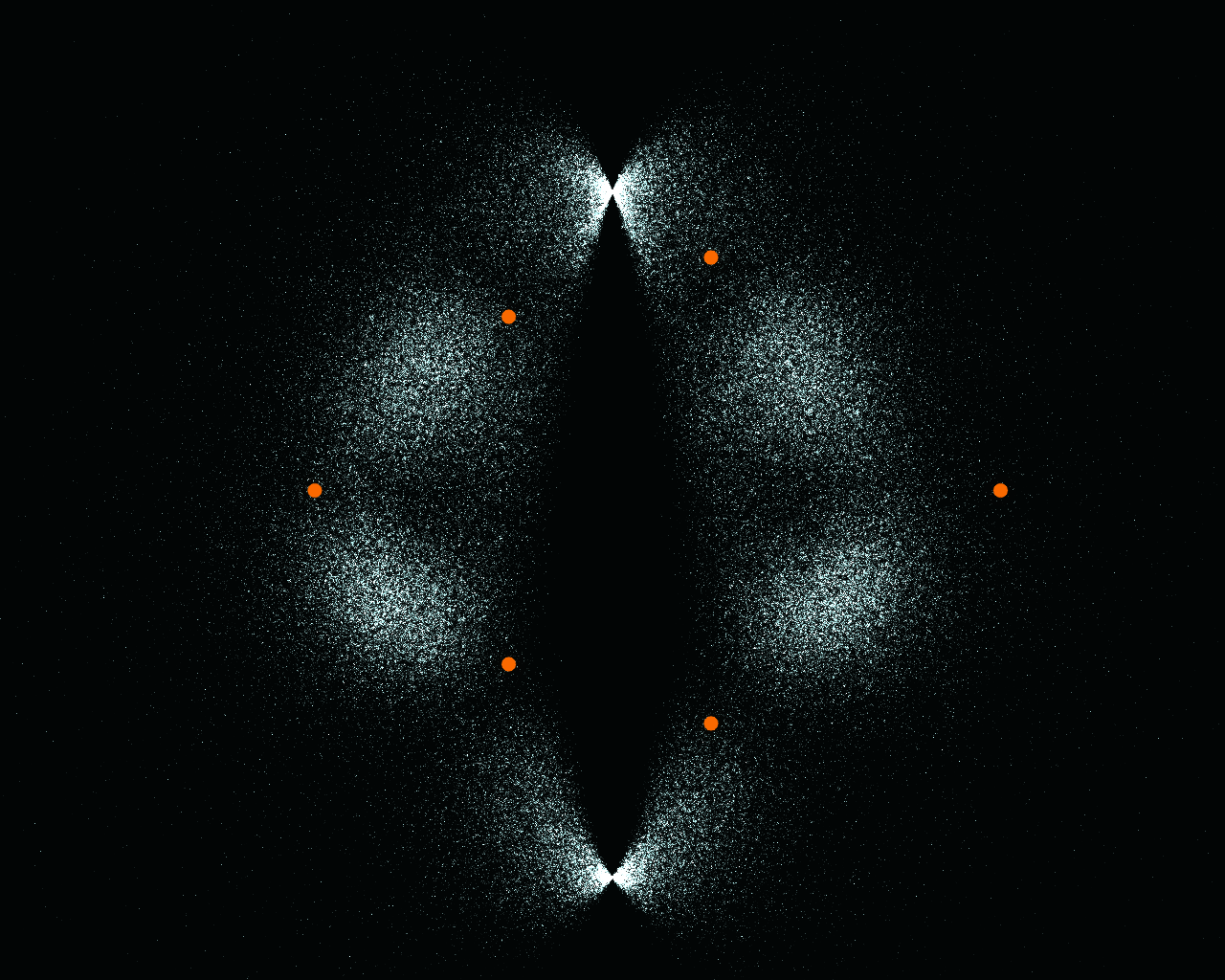
For a given polynomial:
Add random imaginary component:
Questions:
-
Can one compute the distributions of roots?
-
Do other distributions than
give different results?
-
Complex coefficients lead to symmetry breaking, but why so subtle?
-
Is there a better way to color the roots?
Thanks, you!
Contribute, or suggest an issue at
Comment at


